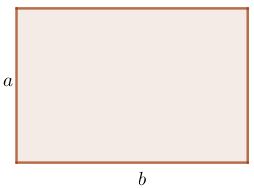Bài 20. Chu vi và diện tích của một số tứ giác đã học
Nội dung lý thuyết
Các phiên bản khác1. CHU VI, DIỆN TÍCH CỦA HÌNH VUÔNG, HÌNH CHỮ NHẬT, HÌNH THANG
Ta đã học và biết sử dụng các công thức tính chu vi, diện tích của hình vuông, hình chữ nhật, hình thang.
| Loại hình | Chu vi | Diện tích |
Hình vuông
| \(C=4a\) | \(S=a^2\) |
Hình chữ nhật
| \(C=2(a+b)\) | \(S=ab\) |
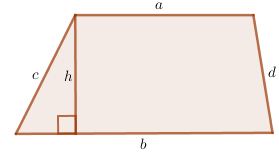
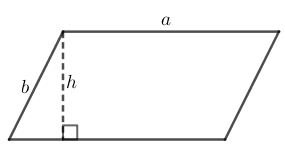
Hình thang
| \(C=a+b+c+d\) | \(S=\frac{1}{2}(a+b)h\) |
(Kí hiệu C là chu vi, S là diện tích của hình)
Ví dụ 1. Bác Khang muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 12 m, chiều rộng 90 m. Loại gạch lát nền được sử dụng là gạch hình vuông có cạnh dài 60 cm. Hỏi bác Khang phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể)?
Giải:
Diện tích nền của căn phòng hình chữ nhật là: 12.9 = 108 (m2).
Diện tích của một viên gạch hình vuông là cạnh 60 cm là:
602 = 3600 (cm2) = 0,36 (m2).
Số viên gạch bác Khang cần dùng là: 108 : 0,36 = 300 (viên).
Ví dụ 2. Một chiếc bàn khung thép được thiết kế như hình dưới. Mặt bàn là hình thang cân có hai đáy lần lượt là 1 400 mm, 600 mm và cạnh bên 800 mm. Chiều cao bàn là 800 mm. Hỏi làm một chiếc khung bàn nói trên cần bao nhiêu mét thép (coi mối hàn không đáng kể)?
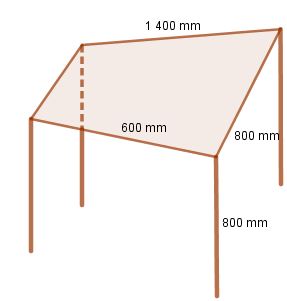
Giải:
Số mét thép để làm khung bàn chính là tổng của chu vi mặt bàn và bốn chân bàn.
Chu vi của mặt bàn là: 1 400 + 800 + 600 + 800 = 3 600 (mm).
Vậy cần số mét thép là:
3 600 + 4.800 = 6 800 (mm) = 6,8 (m).
Ví dụ 3. Một thửa ruộng có dạng như hình dưới.
Nếu trên mỗi mét vuông thu hoạch được 0,9 kg thóc thì thửa ruộng đó thu hoạch được bao nhiêu kilôgam thóc?
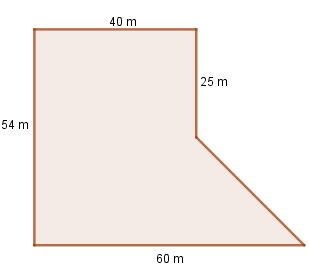
Giải:
Ta chia thửa ruộng thành hai phần gồm hình chữ nhật và hình thang.
.jpg)
Hình chữ nhật ABCD có độ dài hai cạnh là 40 m và 25 m
Diện tích hình chữ nhật ABCD là: 40.25 = 1 000 (m2).
Ta có DE = AE - AD = 54 - 25 = 29 (m).
Hình thang cân DCFE có độ dài hai đáy là 40 m và 60 m, đường cao DE là 29 m.
Diện tích hình thang cân DCFE là: \(\dfrac{1}{2}\cdot\left(40+60\right)\cdot29=1450\) (m2).
Diện tích của cả thửa ruộng là: 1 450 + 1 000 = 2 450 (m2).
Cả thửa ruộng thu hoạch được số kilôgam thóc là: 2 450.0,9 = 2 205 (kg).
@1331958@@1332052@
2. CHU VI, DIỆN TÍCH CỦA HÌNH BÌNH HÀNH, HÌNH THOI
a) Chu vi của hình bình hành, hình thoi
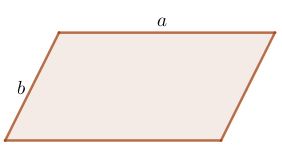
Hình bình hành
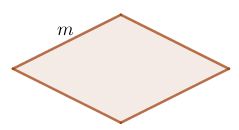
C = 2(a + b) | Hình thoi
C = 4m |
(Kí hiệu C là chu vi của hình)
Ví dụ 1.
a) Tính chu vi của hình thoi có cạnh là 6 cm;
b) Tính chu vi của hình bình hành có độ dài hai cạnh là 5 dm và 40 cm.
Giải:
a) Chu vi của hình thoi là: 4.6 = 24 (cm);
b) Đổi 5 dm = 50 cm.
Chu vi của hình bình hành là: 2.(50 + 40) = 180 (cm).
b) Diện tích hình bình hành
Diện tích hình bình hành là S = ah (a là cạnh, h là chiều cao tương ứng).
(Kí hiệu S là diện tích của hình)
Ví dụ 1. Một tấm bìa có dạng hình bình hành như hình dưới. Tính diện tích của miếng bìa.
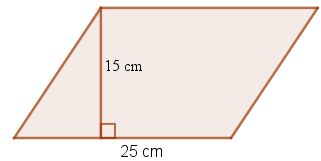
Giải:
Tấm bìa là hình bình hành có chiều cao 15 cm và độ dài cạnh tương ứng là 25 cm nên có diện tích là
S = 15.25 = 375 (cm2).
@1346800@
c) Diện tích hình thoi
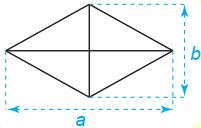
Diện tích hình thoi
\(S=\frac {1}{2} ab\)
\(a, b \ \text{là độ dài hai đường chéo}\).
(Kí hiệu S là diện tích của hình)
Chú ý. Vì hình thoi cũng là hình bình hành nên ta có thể tính diện tích hinh thoi theo công thức tính diện tích hình bình hành S = ah.
Ví dụ 1. Tính diện tích hình thoi có hai đường chéo BD = 20 cm; AC = 14 cm.
Giải:
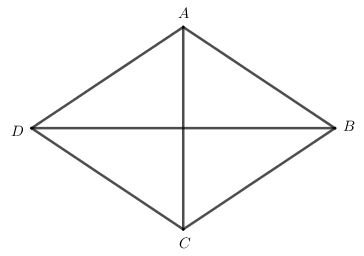
Diện tích hình thoi ABCD là: \(S=\frac{1}{2}.20.14=140 (cm^2)\).
Ví dụ 2. Một mảnh vườn hình chữ nhật có chiều dài 10 m, chiều rộng 8 m. Người ta trồng rau trong một mảnh đất hình thoi như hình dưới. Sau khi thu hoạch người ta tính được trung bình mỗi mét vuông thu được 4 kg rau thì cả mảnh đất hình thoi thu hoạch được bao nhiêu kilôgam rau?
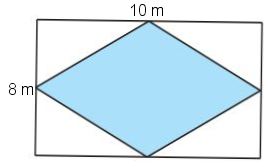
Giải:
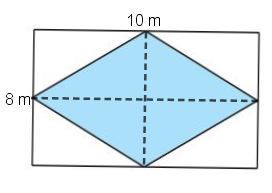
Mảnh đất hình thoi có độ dài hai đường chéo cũng là độ dài hai cạnh của hình chữ nhật.
Diện tích của mảnh đất hình thoi là: S = \(\frac{1}{2}.8.10=40 (m^2)\).
Cả mảnh đất hình thoi thu hoạch được số kilôgam rau là: 4.40 = 160 (kg).
@1346949@