Bài 2: Phương trình lượng giác cơ bản

1. Phương trình \(\sin x=a\)

Xét phương trình \(\sin x=a\) (1)

Trường hợp \(\left|a\right|>1\):

Phương trình (1) vô nghiệm, vì \(\left|\sin x\right|\le1\) với mọi \(x\).

Trường hợp \(\left|a\right|\le1\):

Vẽ đường tròn lượng giác tâm \(O\), trục hoành là trục côsin, trục tung là trục sin. Trên trục sin lấy điểm K sao cho \(\overline{OM}=a\). Từ K kẻ các đường vuông góc với trục sin, cắt đường tròn lượng giác tại M và M' đối xứng nhau qua trục sin (Nếu \(\left|a\right|=1\) thì M trùng với M').

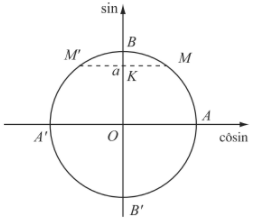
Từ đó ta thấy số đo các cung lượng giác AM và AM' là tất cả các nghiệm của phương trình (1). Gọi \(\alpha\) là số đo bằng radian của một cung lượng giác AM.

Vậy phương trình \(\sin x=a\) có các nghiệm là:

               \(x=\alpha+k2\pi,k\in Z\)  ;

               \(x=\pi-\alpha+k2\pi,k\in Z\).

Nếu số thực \(\alpha\) thoả mãn điều kiện \(\left\{{}\begin{matrix}-\dfrac{\pi}{2}\le\alpha\le\dfrac{\pi}{2}\\\sin\alpha=a\end{matrix}\right.\) thì ta viết \(a=arc\sin\alpha\).

Khi đó các nghiệm của phương trình \(\sin x=a\) được viết là 

               \(x=arc\sin\alpha+k2\pi,k\in Z\)   

        và   \(x=\pi-arc\sin\alpha+k2\pi,k\in Z\).

Chú ý:

a) Phương trình \(\sin x=\sin\alpha\), với \(\alpha\) là một số cho trước, có các nghiệm là

               \(x=\alpha+k2\pi,k\in Z\)  ;

        và   \(x=\pi-\alpha+k2\pi,k\in Z\).

Tổng quát: \(\sin f\left(x\right)=\sin g\left(x\right)\Leftrightarrow\left[{}\begin{matrix}f\left(x\right)=g\left(x\right)+k2\pi,k\in Z\\f\left(x\right)=\pi-g\left(x\right)+k2\pi,k\in Z\end{matrix}\right.\).

b) Phương trình \(\sin x=\sin\beta^o\) có các nghiệm là

              \(x=\beta^o+k360^o,k\in Z\) ;

       và   \(x=180^o-\beta^o+k360^o,k\in Z\).

c) Trong một công thức về nghiệm của phương trình lượng giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

    + \(a=1\): Phương trình \(\sin x=1\) có các nghiệm là \(x=\dfrac{\pi}{2}+k2\pi,k\in Z\).

    + \(a=-1\): Phương trình \(\sin x=-1\) có các nghiệm là \(x=-\dfrac{\pi}{2}+k2\pi,k\in Z\).

    + \(a=0\): Phương trình \(\sin x=0\) có các nghiệm là \(x=k\pi,k\in Z\).

Ví dụ 1: Giải các phương trình:

     a) \(\sin x=\dfrac{1}{2}\)   ;       b) \(\sin x=\dfrac{1}{5}\).

Giải:

a) Vì \(\dfrac{1}{2}=\sin\dfrac{\pi}{6}\) nên \(\sin x=\dfrac{1}{2}\) \(\Leftrightarrow\) \(\sin x=\sin\dfrac{\pi}{6}\)

  Vậy phương trình \(\sin x=\dfrac{1}{2}\) có các nghiệm: \(x=\dfrac{\pi}{6}+k2\pi,k\in Z\)

                                                                   và  \(x=\pi-\dfrac{\pi}{6}+k2\pi=\dfrac{5\pi}{6}+k2\pi,k\in Z\).

b) Ta có \(\sin x=\dfrac{1}{5}\) khi \(x=arc\sin\dfrac{1}{5}\).

   Vậy phương trình \(\sin x=\dfrac{1}{5}\) có các nghiệm: \(x=arc\sin\dfrac{1}{5}+k2\pi,k\in Z\)

                                                                    và  \(x=\pi-arc\sin\dfrac{1}{5}+k2\pi,k\in Z\).

2. Phương trình \(\cos x=a\)

Trường hợp \(\left|a\right|>1\):

Phương trình \(\cos x=a\) vô nghiệm vì \(\left|\cos x\right|\le1\) với mọi \(x\).

Trường hợp \(\left|a\right|\le1\):

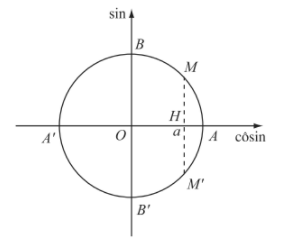
Lấy điểm H trên trục côsin sao cho \(\overline{OH}=a\). Từ H kẻ đường vuông góc với trục côsin, cắt đường tròn lượng giác tại các điểm M và M' đối xứng với nhau qua trục côsin.

Từ đó ta thấy số đo các cung lượng giác AM và AM' là tất cả các nghiệm của phương trình \(\cos x=a\). Gọi \(\alpha\) là số đo bằng radian của một cung lượng giác AM.

Vậy phương trình \(\cos x=a\) có các nghiệm là:

                  \(x=\pm\alpha+k2\pi,k\in Z\)

Chú ý:

a) Phương trình \(\cos x=\cos\alpha\), với \(\alpha\) là một số cho trước, có các nghiệm là

                  \(x=\pm\alpha+k2\pi,k\in Z\).

Tổng quát: \(\cos f\left(x\right)=\cos g\left(x\right)\Leftrightarrow f\left(x\right)=\pm g\left(x\right)+k2\pi,k\in Z\).

b) Phương trình \(\cos x=\cos\beta^o\) có các nghiệm là 

                  \(x=\pm\beta^o+k360^o,k\in Z\).

c) Nếu số thực \(\alpha\) thoả mãn các điều kiện \(\left\{{}\begin{matrix}0\le\alpha\le\pi\\\cos\alpha=a\end{matrix}\right.\) thì ta viết \(\alpha=arc\cos a\)

Khi đó các nghiệm của phương trình \(\cos x=a\) còn được viết là

                 \(x=\pm arc\cos a+k2\pi,k\in Z\).

d) Các trường hợp đặc biệt:

    + \(a=1\): Phương trình \(\cos x=1\) có các nghiệm là \(x=k2\pi,k\in Z\).

    + \(a=-1\): Phương trình \(\cos x=-1\) có các nghiệm là \(x=\pi+k2\pi,k\in Z\).

    + \(a=0\): Phương trình \(\cos x=0\) có các nghiệm là \(x=\dfrac{\pi}{2}+k\pi,k\in Z\).

Ví dụ 2: Giải các phương trình:

           a) \(\cos x=\cos\dfrac{\pi}{6}\)             ;               b) \(\cos3x=-\dfrac{\sqrt{2}}{2}\)      ;

           c) \(\cos x=\dfrac{1}{3}\)                   ;               d) \(\cos\left(x+60^0\right)=\dfrac{\sqrt{2}}{2}\).

Giải:

a) \(\cos x=\cos\dfrac{\pi}{6}\Leftrightarrow\)\(x=\pm\dfrac{\pi}{6}+k\pi,k\in Z\)

b) Vì \(-\dfrac{\sqrt{2}}{2}=\cos\dfrac{3\pi}{4}\) nên \(\cos3x=-\dfrac{\sqrt{2}}{2}\) \(\Leftrightarrow\) \(\cos3x=\cos\dfrac{3\pi}{4}\)

    \(\Leftrightarrow3x=\pm\dfrac{3\pi}{4}+k2\pi,k\in Z\)

    \(\Leftrightarrow x=\pm\dfrac{\pi}{4}+k\dfrac{2\pi}{3},k\in Z\).

c) \(\cos x=\dfrac{1}{3}\) \(\Leftrightarrow\) \(x=\pm arc\cos\dfrac{1}{3}+k2\pi,k\in Z\)

d) Vì \(\dfrac{\sqrt{2}}{2}=\cos45^o\) nên \(\cos\left(x+60^0\right)=\dfrac{\sqrt{2}}{2}\) \(\Leftrightarrow\) \(\cos\left(x+60^o\right)=\cos45^o\)

    \(\Leftrightarrow\) \(x+60^o=\pm45^o+k360^o,k\in Z\)

    \(\Leftrightarrow\) \(\left[{}\begin{matrix}x=-15^o+k360^o\\x=-105^o+k360^o\end{matrix}\right.,k\in Z\)

3. Phương trình \(\tan x=a\)

Điều kiện của phương trình là \(x\ne\dfrac{\pi}{2}+k\pi(k\in Z)\).

Căn cứ vào đồ thị hàm số \(y=\tan x\), ta thấy với mỗi số \(\alpha\), đồ thị \(y=\tan x\) cắt đường thẳng \(y=a\) tại các điểm có hoành độ sai khác nhau một bội của \(\pi\).

Hoành độ của mỗi giao điểm là một nghiệm của phương trình \(\tan x=a\).

Gọi \(x_1\) là hoành độ giao điểm (\(\tan x_1=a\)) thoả mãn \(-\dfrac{\pi}{2}< x_1< \dfrac{\pi}{2}\).

Kí hiệu \(x_1=arc\tan a\).

Khi đó nghiệm của phương trình \(\tan x=a\) là

               \(x=arc\tan a+k\pi,k\in Z\).

Chú ý:

a) Phương trình \(\tan x=\tan\alpha\) với \(\alpha\) là một số cho trước có các nghiệm là

               \(x=\alpha+k\pi,k\in Z\).

Tổng quát: \(\tan f\left(x\right)=\tan g\left(x\right)\Leftrightarrow f\left(x\right)=g\left(x\right)+k\pi,k\in Z\)

b) Phương trình \(\tan x=\tan\beta^o\) có các nghiệm là 

               \(x=\beta^o+k180^o,k\in Z\).

Ví dụ 3: Giải các phương trình:

        a) \(\tan x=\tan\dfrac{\pi}{5}\)     ;     b) \(\tan2x=-\dfrac{1}{3}\)       ;        c) \(\tan\left(3x+15^o\right)=\sqrt{3}\)

Giải:

a) \(\tan x=\tan\dfrac{\pi}{5}\) \(\Leftrightarrow\) \(x=\dfrac{\pi}{5}+k\pi,k\in Z\)

b) \(\tan2x=-\dfrac{1}{3}\) \(\Leftrightarrow\) \(2x=arc\tan\left(-\dfrac{1}{3}\right)+k\pi,k\in Z\)

                          \(\Leftrightarrow\) \(x=arc\tan\left(-\dfrac{1}{3}\right)+k\dfrac{\pi}{2},k\in Z\)

c) Vì \(\sqrt{3}=\tan60^o\) nên \(\tan\left(3x+15^o\right)=\sqrt{3}\) \(\Leftrightarrow\) \(\tan\left(3x+15^o\right)=\tan60^o\)

   \(\Leftrightarrow\) \(3x+15^o=60^o+k180^o,k\in Z\)

   \(\Leftrightarrow\) \(3x=45^o+k180^o,k\in Z\)

   \(\Leftrightarrow\) \(x=15^o+k60^o,k\in Z\).

4. Phương trình \(\cot x=a\)

Điều kiện của phương trình là \(x\ne k\pi,k\in Z\).

Phương trình \(\cot x=a\) có các nghiệm là

               \(x=arc\cot a+k\pi,k\in Z\)

Chú ý:

a) Phương trình \(\cot x=\cot\alpha\), với \(\alpha\) là một số cho trước, có các nghiệm là

              \(x=\alpha+k\pi,k\in Z\).

Tổng quát: \(\cot f\left(x\right)=\cot g\left(x\right)\Leftrightarrow f\left(x\right)=g\left(x\right)+k\pi,k\in Z\)

b) Phương trình \(\cot x=\cot\beta^o\) có các nghiệm là

              \(x=\beta^o+k180^o,k\in Z\).

Ví dụ 4: Giải các phương trình:

        a) \(\cot4x=\cot\dfrac{2\pi}{7}\)   ;      b) \(\cot3x=-2\)      ;        c) \(\cot\left(2x-10^o\right)=\dfrac{1}{\sqrt{3}}\)

Giải:

a) \(\cot4x=\cot\dfrac{2\pi}{7}\) \(\Leftrightarrow\) \(4x=\dfrac{2\pi}{7}+k\pi,k\in Z\)

                               \(\Leftrightarrow\) \(x=\dfrac{\pi}{14}+k\dfrac{\pi}{4},k\in Z\)

b) \(\cot3x=-2\) \(\Leftrightarrow\) \(3x=arc\cot\left(-2\right)+k\pi,k\in Z\)

                        \(\Leftrightarrow\) \(x=\dfrac{1}{3}arc\cot\left(-2\right)+k\dfrac{\pi}{3},k\in Z\)

c) Vì \(\dfrac{1}{\sqrt{3}}=\cot60^o\) nên

    \(\cot\left(2x-10^o\right)=\dfrac{1}{\sqrt{3}}\) \(\Leftrightarrow\) \(\cot\left(2x-10^o\right)=\cot60^o\)

   \(\Leftrightarrow\) \(2x-10^o=60^o+k180^o,k\in Z\)

   \(\Leftrightarrow\) \(x=35^o+k90^o,k\in Z\).

Ghi nhớ:

Mỗi phương trình \(\sin x=a\) (\(\left|a\right|\le1\)), \(\cos x=a\) (\(\left|a\right|\le1\)), \(\tan x=a\) (\(\left|a\right|\le1\)) và \(\cot x=a\) (\(\left|a\right|\le1\)) có vô số nghiệm.

Giải các phương trình trên là tìm tất cả các nghiệm của chúng.