Bài 2. Hình chữ nhật. Hình thoi. Hình bình hành - Hình thang cân
Nội dung lý thuyết
Các phiên bản khác1. Hình chữ nhật
Hình chữ nhật ABCD có:
| 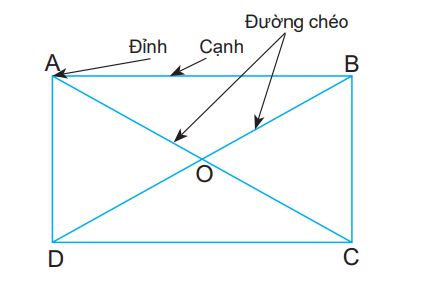 |
Ví dụ. Cho hình chữ nhật ABCD có AD = 8 cm; AC = 14 cm. Tính BC, BD.
Giải:
Hình chữ nhật có cặp cạnh đối diện bằng nhau nên BC = AD = 8 cm.
Hình chữ nhật có hai đường chéo bằng nhau nên BD = AC = 14 cm.
Vẽ hình chữ nhật
Để vẽ hình chữ nhật ABCD có AB = 7 cm, AD = 5 cm ta làm theo các bước sau:
Bước 1: Vẽ đoạn thẳng AB = 7 cm và đoạn thẳng AD = 5 cm vuông góc với nhau. Bước 2: Qua B vẽ đường thẳng vuông góc với AB. Bước 3: Qua D vẽ đường thẳng vuông góc với AD. Hai đường thẳng này cắt nhau tại C. ABCD là hình chữ nhật cần vẽ. | 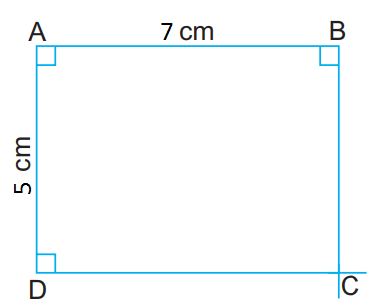 |
@1612111@
2. Hình thoi
Hình thoi ABCD có:
|  |
Vẽ hình thoi
Để vẽ hình thoi ABCD khi biết AB = 8 cm và đường chéo AC = 10 cm ta làm như sau:
- Vẽ đoạn thẳng AC = 10 cm.
- Lấy A và C làm tâm, vẽ hai đường tròn bán kính 8 cm, hai đường tròn này cắt nhau tại hai điểm B và D.
- Nối B với A, B với C, D với A, D với C.
ABCD là hình thoi cần vẽ.

@1612162@
3. Hình bình hành
Hình bình hành ABCD có:
|  |
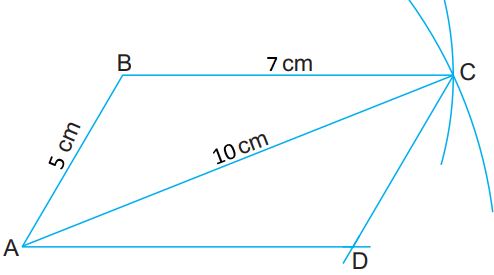
Vẽ hình bình hành
Để vẽ hình bình hành ABCD với AB = 5 cm, BC = 7 cm và đường chéo AC = 10 cm ta làm như sau:
- Vẽ đoạn thẳng AB = 5 cm.
- Vẽ đường tròn tâm A bán kính 10 cm; vẽ đường tròn tâm B bán kính 7 cm; hai đường tròn cắt nhau tại C. Nối B với C.
- Từ A kẻ đường thẳng song song với BC; từ C kẻ đường thẳng song song với AB; hai đường thẳng này cắt nhau tại D.
ABCD là hình bình hành cần vẽ.
@1620043@
4. Hình thang cân
Hình thang cân ABCD có:
|  |
Ví dụ. Cho hình thang cân MNPQ có MQ = 9 cm; MP = 16 cm, góc MNP bằng 130o. Tính MQ, MP, số đo góc QMN.
Giải:

Hình thang cân có:
- hai cạnh bên bằng nhau nên MQ = NP = 9 cm.
- có hai đường chéo bằng nhau nên MP = NQ = 16 cm.
- hai góc kề một đáy bằng nhau nên góc MNP = góc QMN = 130o.
@1620130@