Bài 1. Hình vuông - Tam giác đều - Lục giác đều
Nội dung lý thuyết
Các phiên bản khác1. Hình vuông
Hình vuông ABCD là hình có:
|
|
Lưu ý: Hai đường chéo của hình vuông bằng nhau.
Vẽ hình vuông
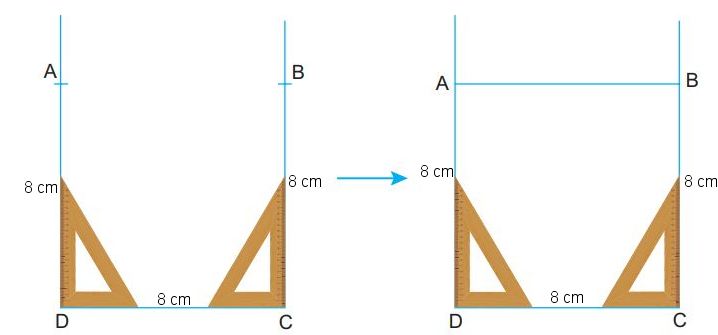
Ta vẽ hình vuông cạnh 8 cm bằng thước kẻ và êke theo hướng dẫn sau:
- Vẽ đoạn thẳng CD dài 8 cm.
- Vẽ hai đường thẳng vuông góc với CD tại C và D như hình vẽ.
- Trên đường thẳng qua C lấy đoạn thẳng CB = 8 cm; trên đường thẳng qua D lấy đoạn thẳng DA = 8 cm.
- Nối hai điểm A và B ta được hình vuông cần vẽ.
- Dùng thước và êke để kiểm tra xem hình ABCD có các cạnh bằng nhau không, có các góc bằng nhau không.
@1595350@
2. Tam giác đều
Tam giác đều ABC có:
|  |
Vẽ tam giác đều
Để vẽ tam giác đều ABC cạnh 5 cm bằng thước và compa ta làm như sau:
- Vẽ đoạn thẳng AB = 5 cm.
- Lấy A, B làm tâm, vẽ hai đường tròn bán kính 5 cm.
Gọi C là một trong hai giao điểm của hai đường tròn. Nối C với A và C với B ta được tam giác đều ABC.

@1595449@
3. Lục giác đều
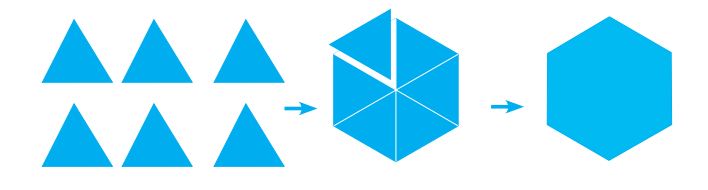
Ghép 6 tam giác đều như hình, ta được một hình lục giác đều.
Hình lục giác đều ABCDEF có:
|  |
Lưu ý: Trong hình lục giác đều, ba đường chéo chính bằng nhau.
Ví dụ. Cho hình lục giác đều ABCDEF có AD = 9 cm. Tính độ dài các cạnh CF, BE.
Giải:
Vì hình lục giác đều có các đường chéo chính bằng nhau nên CF = BE = AD = 9 cm.
.jpg)