Bài 1: Hệ tọa độ trong không gian
Nội dung lý thuyết
Các phiên bản khácI. TOẠ CỦA ĐIỂM VÀ CỦA VECTƠ
1. Hệ toạ độ
Trong không gian, các trục \(x'Ox,y'Oy,z'Oz\) vuông góc với nhau từng đôi một. Gọi \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\) lần lượt là các vectơ đơn vị trên các trục \(x'Ox,y'Oy,z'Oz\).
Hệ ba trục như vậy được gọi là hệ trục toạ độ Đề-các vuông góc \(Oxyz\) trong không gian, hay được gọi đơn giản là hệ toạ độ \(Oxyz\).
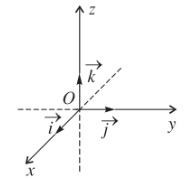
Điểm \(O\) được gọi là gốc toạ độ.
Các mặt phẳng \(\left(Oxy\right),\left(Oyz\right),\left(Ozx\right)\) đôi một vuông góc với nhau được gọi là các mặt phẳng toạ độ.
Vì \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\) là ba vectơ đơn vị đôi một vuông góc với nhau nên
\(\overrightarrow{i}^2=\overrightarrow{j}^2=\overrightarrow{k}^2=1\)
và \(\overrightarrow{i}.\overrightarrow{j}=\overrightarrow{j}.\overrightarrow{k}=\overrightarrow{k}.\overrightarrow{i}=0\)
2. Toạ độ của một điểm
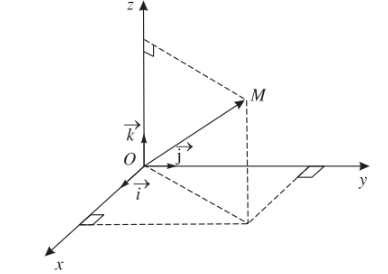
Toạ độ của điểm \(M\) đối với hệ trục toạ độ \(Oxyz\) là bộ ba số \(\left(x;y;z\right)\) duy nhất sao cho \(\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}\)
Ta viết: \(M\left(x;y;z\right)\) hoặc \(M=\left(x;y;z\right)\).
3. Toạ độ của vectơ
Trong không gian \(Oxyz\) cho vectơ \(\overrightarrow{a}\). Khi đó luôn tồn tại duy nhất bộ ba số \(\left(a_1;a_2;a_3\right)\) sao cho \(\overrightarrow{a}=a_1\overrightarrow{i}+a_2\overrightarrow{j}+a_3\overrightarrow{k}\).
Ta gọi bộ ba số \(\left(a_1;a_2;a_3\right)\) là toạ độ vectơ \(\overrightarrow{a}\) đối với hệ toạ độ \(Oxyz\) cho trước và viết \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\) hoặc \(\overrightarrow{a}\left(a_1;a_2;a_3\right)\).
Nhận xét: Trong hệ toạ độ \(Oxyz\), toạ độ điểm \(M\) chính là toạ độ vectơ \(\overrightarrow{OM}\).
Ta có \(M=\left(x;y;z\right)\Leftrightarrow\overrightarrow{OM}=\left(x;y;z\right)\).
II. BIỂU THỨC TOẠ ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ
Định lí:
Trong không gian \(Oxyz\) cho hai vectơ \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\) và \(\overrightarrow{b}=\left(b_1;b_2;b_3\right)\). Ta có:
\(\overrightarrow{a}+\overrightarrow{b}=\left(a_1+b_1;a_2+b_2;a_3+b_3\right)\) ;
\(\overrightarrow{a}-\overrightarrow{b}=\left(a_1-b_1;a_2-b_2;a_3-b_3\right)\) ;
\(k\overrightarrow{a}=k\left(a_1;a_2;a_3\right)=\left(ka_1;ka_2;ka_3\right)\) với \(k\) là một số thực.
Hệ quả:
a) Cho hai vectơ \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\) và \(\overrightarrow{b}=\left(b_1;b_2;b_3\right)\).
Ta có: \(\overrightarrow{a}=\overrightarrow{b}\Leftrightarrow\left\{{}\begin{matrix}a_1=b_1\\a_2=b_2\\a_3=b_3\end{matrix}\right.\).
b) Vectơ \(\overrightarrow{0}\) có toạ độ là \(\left(0;0;0\right)\).
c) Với \(\overrightarrow{b}\ne\overrightarrow{0}\) thì hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng phương khi và chỉ khi có một số thực \(k\) sao cho \(a_1=kb_1,a_2=kb_2,a_3=kb_3\).
d) Trong không gian nếu cho hai điểm \(A\left(x_A;y_A;z_A\right)\) và \(B\left(x_B;y_B;z_B\right)\) thì:
\(\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\left(x_B-x_A;y_B-y_A;z_B-z_A\right)\)
Toạ độ trung điểm \(M\) của đoạn thẳng \(AB\) là \(M\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2};\dfrac{z_A+z_B}{2}\right)\).
Ví dụ 1: Cho ba vectơ \(\overrightarrow{a}=\left(2;-5;3\right),\overrightarrow{b}=\left(0;2;-1\right),\overrightarrow{c}=\left(1;7;2\right)\). Tính toạ độ của vectơ \(\overrightarrow{d}=4\overrightarrow{a}-\dfrac{1}{3}\overrightarrow{b}+3\overrightarrow{c}\).
Giải:
Ta có: \(\overrightarrow{d}=4\overrightarrow{a}-\dfrac{1}{3}\overrightarrow{b}+3\overrightarrow{c}\)
\(=4\left(2;-5;3\right)-\dfrac{1}{3}\left(0;2;-1\right)+3\left(1;7;2\right)\)
\(=\left(8;-20;12\right)-\left(0;\dfrac{2}{3};-\dfrac{1}{3}\right)+\left(3;21;6\right)\)
\(=\left(11;\dfrac{1}{3};\dfrac{55}{3}\right)\)
Vậy \(\overrightarrow{d}=\left(11;\dfrac{1}{3};\dfrac{55}{3}\right)\).
@2603875@
III. TÍCH VÔ HƯỚNG
1. Biểu thức toạ độ của tích vô hướng
Trong không gian \(Oxyz\), tích vô hướng của hai vectơ \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\) và \(\overrightarrow{b}=\left(b_1;b_2;b_3\right)\) được xác định bởi công thức:
\(\overrightarrow{a}.\overrightarrow{b}=a_1b_1+a_2b_2+a_3b_3\)
2. Ứng dụng
a) Độ dài của vectơ
Cho vectơ \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\). Độ dài của vectơ \(\overrightarrow{a}\) là \(\left|\overrightarrow{a}\right|=\sqrt{a_1^2+a_2^2+a_3^2}\).
b) Khoảng cách giữa hai điểm
Trong không gian cho hai điểm \(A\left(x_A;y_A;z_A\right)\) và \(B\left(x_B;y_B;z_B\right)\). Khoảng cách giữa hai điểm này chính là độ dài vectơ \(\overrightarrow{AB}\), ta có:
\(AB=\left|\overrightarrow{AB}\right|=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2+\left(z_B-z_A\right)^2}\)
c) Góc giữa hai vectơ
Nếu \(\varphi\) là góc giữa hai vectơ \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\) và \(\overrightarrow{b}=\left(b_1;b_2;b_3\right)\) với \(\overrightarrow{a},\overrightarrow{b}\ne\overrightarrow{0}\) thì \(\cos\varphi=\dfrac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}\). Do đó: \(\cos\varphi=\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_1^2+a_2^2+a_2^3}.\sqrt{b_1^2+b_2^2+b_3^2}}\).
Từ đó suy ra \(\overrightarrow{a}\perp\overrightarrow{b}\Leftrightarrow a_1b_1+a_2b_2+a_3b_3=0\).
Ví dụ 2: Tính \(\overrightarrow{a}.\overrightarrow{b}\) với \(\overrightarrow{a}=\left(3;0;6\right)\) và \(\overrightarrow{b}=\left(2;-4;0\right)\).
Giải:
Với \(\overrightarrow{a}=\left(3;0;6\right)\) và \(\overrightarrow{b}=\left(2;-4;0\right)\) ta có:
\(\overrightarrow{a}.\overrightarrow{b}=3.6+0.\left(-4\right)+6.0=18\).
@2603821@@58531@
IV. PHƯƠNG TRÌNH MẶT CẦU
Định lí:
Trong không gian \(Oxyz\), mặt cầu \(\left(S\right)\) tâm \(I\left(a;b;c\right)\) bán kính \(r\) có phương trình là:
\(\left(x-a\right)^2+\left(y-b\right)^2+\left(z-c\right)^2=r^2\).
Nhận xét: Phương trình mặt cầu có thể được viết dưới dạng
\(x^2+y^2+z^2-2ax-2by-2cz+d=0\) với \(d=a^2+b^2+c^2-r^2\).
Ví dụ 3: Xác định tâm và bán kính của mặt cầu có phương trình
\(x^2+y^2+z^2+4x-2y+6z+5=0\).
Giải:
Phương trình mặt cầu đã cho tương ứng với phương trình \(\left(x+2\right)^2+\left(y-1\right)^2+\left(z+3\right)^2=3^2\)
Vậy mặt cầu đã cho có tâm \(I\left(-2;1;-3\right)\) và có bán kính \(r=3\).
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn