Một con lắc lò xo dao động điều hòa với đồ thị phụ thuộc động năng và thế năng vào li độ như hình vẽ. Biết m omega^2 = 100. Tính giá trị của W0.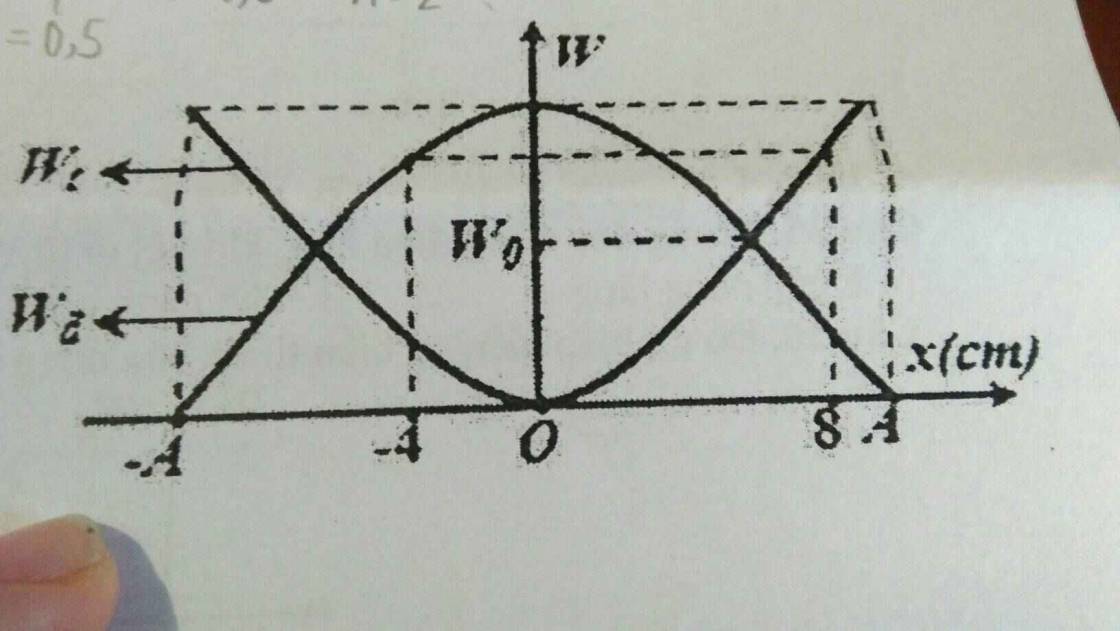
Chương I- Điện tích. Điện trường
Một vật dao động điều hòa dọc theo trục Ox quanh điểm gốc O ,với biên độ 4cm,tần số f=5Hz.tại thời điểm t=0,vật qua vị trí có li độ x=-4cm
a.Viết phương trình dao động của vật
b.Xác định thời điểm đầu tiên vật qua vị trí có li độ x=-2√3cm
c.Tính quãng đường vật đi được trong 2s kể từ lúc t=0
`a)A=4 (cm)`
`\omega=2\pi .f=10\pi (rad//s)`
Tại `t=0` thì `x_0 =-4=>\varphi=\pi (rad)`
`=>` Ptr: `x=4cos(10\pi t+\pi)`.
`b)` Ta có: `t=T/4 -T/6=T/12 =1/12 . [2\pi]/[10\pi]=1/60 (s)`
`c)T=[2\pi]/[10\pi]=0,2(s)`
`=>` Trong `2s` vật đi được `t=2/[0,2]=10T`
`=>` Quãng đường đi được trong `2s` là: `s=10.4.A=160(cm)`.
Đúng 2
Bình luận (0)
Một vật dao động trên quỹ đạo thẳng có chiều dài 10cm,tần số 2,5Hz.tại thời điểm ban đầu (t=0).viết phương trình dao động của vật nếu tại thời điểm(t=0)
a.vật qua vị trí cân bằng theo chiều dương
b.vật tại vị trí cân bằng theo chiều âm
c.vật qua vị trí có li độ 2,5 cm theo chiều âm
d.vật qua vị trí có li độ -2,5 cm theo chiều dương
`A=L/2=10/2=5(cm)`
`\omega =2\pi .f=5\pi(rad//s)`
`a)` Tại `t=0`, vật đi qua VTCB theo chiều dương `=>\varphi =-\pi/2`
`=>` Ptr: `x=5cos(5\pi t-\pi/2)`.
_____
`b)` Tại `t=0`, vật đi qua VTCB theo chiều âm `=>\varphi =\pi/2`
`=>` Ptr: `x=5cos(5\pi t+\pi/2)`
______
`c)` Tại `t=0`, vật qua vị trí có li độ `2,5 cm` theo chiều âm `=>\varphi=\pi/3`
`=>` Ptr: `x=5cos(5\pi+\pi/3)`.
______
`d)` Tại `t=0`, vật qua vị trí có li độ `2,5 cm` theo chiều dương `=>\varphi =-pi/3`
`=>` Ptr: `x=5cos(5\pi -\pi/3)`.
Đúng 1
Bình luận (0)
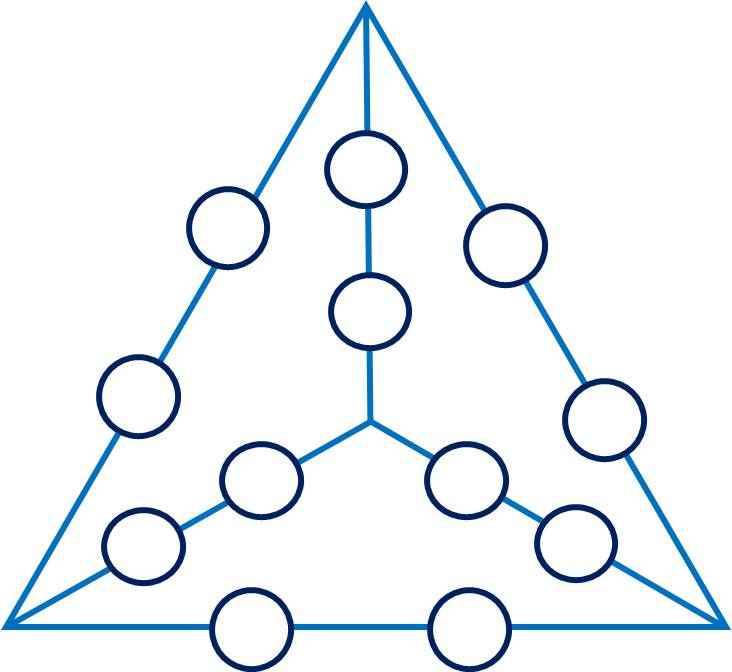
Cho hình tứ diện đều như hình vẽ (góc nhìn từ trên xuống). Mỗi cạnh của tứ diện có hai ô trống tròn. 1. Khi đó tổng mỗi mặt của tứ diện là bao nhiêu?2. Điền số tự nhiên từ 1 đến 12 sao cho tổng mỗi mặt bằng nhau.
Đọc tiếp
Cho hình tứ diện đều như hình vẽ (góc nhìn từ trên xuống). Mỗi cạnh của tứ diện có hai ô trống tròn.
1. Khi đó tổng mỗi mặt của tứ diện là bao nhiêu?
2. Điền số tự nhiên từ 1 đến 12 sao cho tổng mỗi mặt bằng nhau.
Để giải bài toán này, ta cần xác định giá trị của các ô trống tròn trên mỗi cạnh của tứ diện đều.
Đầu tiên, ta xác định giá trị của mỗi mặt của tứ diện. Vì tứ diện đều có 4 mặt, ta cần tìm tổng của các ô trống tròn trên mỗi mặt. Do đó, tổng mỗi mặt của tứ diện là tổng giá trị của cả 4 ô trống tròn trên mỗi cạnh.
Để điền số tự nhiên từ 1 đến 12 sao cho tổng mỗi mặt bằng nhau, ta có thể sử dụng phương pháp thử và sai. Ta có thể bắt đầu bằng việc điền các số từ 1 đến 12 vào các ô trống tròn trên mỗi cạnh, và sau đó kiểm tra xem tổng mỗi mặt có bằng nhau hay không.
Dưới đây là một cách điền số để tổng mỗi mặt bằng nhau:
6 1 52 4 3 12
Trong trường hợp này, tổng mỗi mặt sẽ là 1 + 2 + 6 + 3 = 12.
Vì vậy, tổng mỗi mặt của tứ diện đều là 12.
Đúng 0
Bình luận (0)
Vật dao động điều hòa với biên độ A, thời gian ngắn nhất vật đi từ vị trí cân bằng đến li độ x = \(\dfrac{-A}{2}\) là 0,1 s. Chu kì dao động của vật bằng
Thời gian ngắn nhất để vật đi từ VTCB đến li độ \(x=-\dfrac{A}{2}\) là \(\dfrac{T}{12}\)
\(\Rightarrow\dfrac{T}{12}=0,1\Rightarrow T=1,2\left(s\right)\)
Đúng 2
Bình luận (0)
Một vật dao động điều hòa với tần số góc là 40rad/s. Khi vật cách vị trí câu bằng 24 cm thì vật có tốc độ là 2,8 m/s. Vật dao động với biên độ bằng
Ta có: \(x^2+\dfrac{v^2}{w^2}=A^2\)
\(\Rightarrow A^2=0,24^2+\dfrac{2,8^2}{40^2}=\dfrac{1}{16}\\ \Rightarrow A=0,25\left(m\right)=25cm\)
Đúng 1
Bình luận (0)
một chất điểm dao động điều hòa theo pt x=4cos(\(\dfrac{2\pi t}{3}\)) (x tính bằng cm, t tính bằng s). kể từ t=0 chất điểm đi qua vị trí có li độ x=-2cm lần thứ 2011 tại thời điểm?
Ta có: \(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\dfrac{2\pi}{3}}=3\left(s\right)\)
Thời gian vật đi từ vị trí có li độ x = 4 cm đến vị trí có li độ x = -2 lần đầu tiên là:
\(t_1=\dfrac{T}{4}+\dfrac{T}{12}=\dfrac{3}{4}+\dfrac{3}{12}=1\left(s\right)\)
Thời gian vật đi qua vị trí có li độ x = -2 lần thứ 2 đến vị trí có li độ x = -2 lần thứ 2011 là:
\(t_2=1005\cdot T=1005\cdot3=3015\left(s\right)\)
Tổng thời gian cần là: \(t=t_1+t_2=1+3015=3016\left(s\right)\)
Đúng 3
Bình luận (0)
một vật dao động điều hào với pt x=4cos(\(4\pi t+\dfrac{\pi}{6}\)) (cm) vật qua vị trí có li độ x=2cm lần thứ 2013 vào thời điểm bao nhiêu
Do ban đầu vật ở vị trí có pha là \(\dfrac{\pi}{6}\)
⇒ Thời gian để vật đi qua vị trí có li độ x = 2 cm lần thứ nhất là
\(\dfrac{T}{12}=\dfrac{2\pi}{12w}=\dfrac{2\pi}{12\cdot4\pi}=\dfrac{1}{24}\left(s\right)\)
Thời gian để vật đi qua vị trí có li độ x = 2 cm lần thứ 2 đến lần thứ 2013 là
\(\dfrac{2012}{2}\cdot T=\dfrac{2012}{2}\cdot\dfrac{1}{2}=503\left(s\right)\)
Vậy tổng thời gian là \(503+\dfrac{1}{24}\simeq503,042\left(s\right)\)
Đúng 3
Bình luận (0)
Một vật nhỏ dao động điều hòa dọc theo trục Ox (vị trí cân bằng trùng với O) với biên độ 4 cm và tần số 10 Hz. Tại thời điểm t = 0, vật qua vị trí cân bằng theo chiều dương của trục Ox. Phương trình dao động của vật là bao nhiêu
Có: \(f=\dfrac{w}{2\pi}=10\Rightarrow w=20\pi\)
Phương trình dao động của vật là:
\(x=4cos\left(20\pi t-\dfrac{\pi}{2}\right)\)
Đúng 3
Bình luận (0)
Một vật dao động điều hoà theo phương trình x = 10cos(\(\pi t+\dfrac{\pi}{3}\)) cm. Thời gian tính từ lúc vật bắt đầu dao động động (t = 0) đến khi vật đi được quãng đường 30 cm là bao nhiêu
\(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\pi}=2\left(s\right)\)
Trong 1 nửa chu kì, vật di chuyển được quãng đường là \(2\cdot10=20\left(cm\right)\)
Vật khi đó phải đi từ vị trí có pha bằng \(-\dfrac{\pi}{3}\) đến vị trí có pha bằng \(\dfrac{\pi}{3}\), vì vật sẽ di chuyển được quãng đường \(\dfrac{A}{2}+\dfrac{A}{2}=A=10\left(cm\right)\)
Vậy thời gian vật phải đi là: \(\dfrac{T}{2}+\dfrac{T}{6}=\dfrac{2}{2}+\dfrac{2}{6}=\dfrac{4}{3}\left(s\right)\)
Đúng 2
Bình luận (0)


