cho tam giác ABC cân tại A , gọi M là trung điểm BC
a)chứng minh tam giác ABM=tam giác ACM
b)trên cạnh AM lấy điểm K bất kỳ, chứng minh rằng KB = KC
c)tia BK cắt cạnh AC tại F, tia CK cắt cạnh AB tại E . chúng minh EF//BC
Bài 7: Tính chất đường trung trực của một đoạn thẳng
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
=>KM\(\perp\)BC
Xét ΔKBC có
KM là đường cao
KM là đường trung tuyến
Do đó:ΔKBC cân tại K
=>KB=KC
c: ΔKBC cân tại K
=>\(\widehat{KBC}=\widehat{KCB}\)
\(\widehat{ABF}+\widehat{FBC}=\widehat{ABC}\)
\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)
mà \(\widehat{FBC}=\widehat{ECB}\)
và \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABF}=\widehat{ACE}\)
=>\(\widehat{EBK}=\widehat{FCK}\)
Xét ΔEBK và ΔFCK có
\(\widehat{EBK}=\widehat{FCK}\)
BK=CK
\(\widehat{EKB}=\widehat{FKC}\)
Do đó: ΔEBK=ΔFCK
Đúng 4
Bình luận (0)
Cho tam giác ABC cân tại A có d là đường trung trực AB vẽ phân giác AE của góc BAC ( E thuộc BC ) d cắt AE tại O a, AE là đường trung trực của tam giác ABC b, O thuộc đường trung trực của đoạn thẳng AC c, O cách đều 3 đỉnh của tam giác ABC
a: ΔABC cân tại A
mà AE là phân giác
nên AE là trung trực của BC
b: O nằm trên trung trực của AB
=>OA=OB
O nằm trên trung trực của BC
=>OB=OC
=>OA=OC
=>O nằm trên trung trực của AC
c: OA=OB=OC
=>O cách đều 3 đỉnh của ΔABC
Đúng 1
Bình luận (0)
Cho tam giác ABC có AC = 2AB. Trên cạnh AC lấy điểm M sao cho AM = AB. Trên tia đối của tia BA lấy điểm D sao cho BA = BD. Gọi K là giao điểm của DM và BC.
a,so sánh AK và AC
b, Chứng minh rằng KB = 1/2 KC
c, Qua C kẻ đường thẳng song song với AD, qua D kẻ đường thẳng song song với AC chúng cắt nhau tại E. Chứng minh rằng A, K, E thẳng hàng.
Cho tam giác ABC vuông tại A, AB<AC. Tia phân giác của góc ABC cắt cạnh AC tại D. Kẻ DE vuông góc với BC
a) Chứng minh AB=BE.
b) Chứng minh BD là đường trung trực của AE.
c) Tia ED vắt tia BA tại điểm K. Chứng minh °DKC cân và DA<DC.
d) Chứng minh BD vuông góc với CK .
Cho tam giác cân ABC có AB=AC . Hai đường trung trực của hai cạnh AB;AC
cắt nhau tại O . Chứng minh AOB=AOC .
cho 2 đường thẳng xx' và yy' cắt nhau tại O. Trên tia Ox lấy 2 điểm A,B sao cho A nằm giữa B, AB= 2OA.Trên yy' lấy 2 điểm L và M sao cho O là trung điểm của LM.Nối B với L, B với M và gọi P là trung điểm của đoạn MB,Q là trung điểm của đoạn LB. Chứng minh rằng các đoạn thẳng LP và MQ đi qua A.
Xet ΔBML có
P,Q lần lươt là trung điểm của BM,BL
=>LP cắt MQ tại trọng tâm của ΔBML
Xét ΔBML có
BO là trung tuyến
BA=2/3BO
=>A la trọng tâm
=>LP cắt MQ tại A
Đúng 0
Bình luận (0)
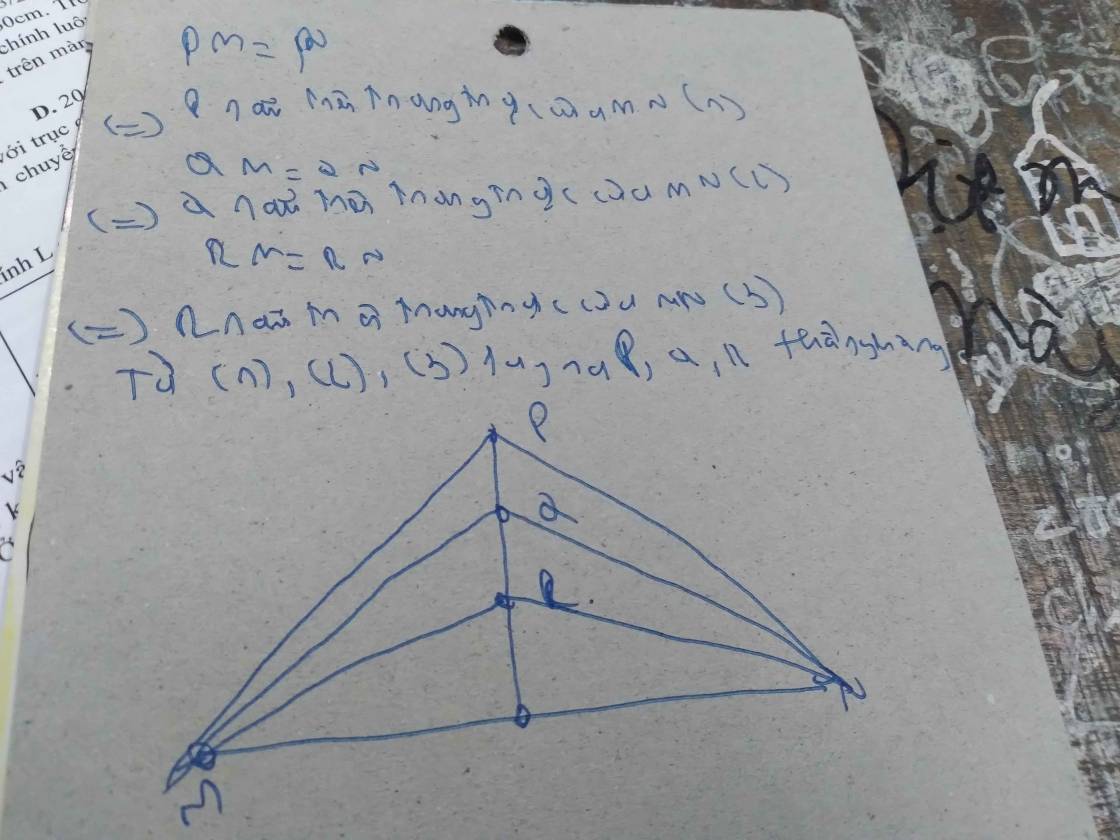
Cho đoạn thẳng MN, vẽ 3 điểm P, Q, R không thuộc MN sao cho PM=PN, QM=QN, RM=RN.Chứng Minh:P, Q, R thẳng hàng
giúp mik với nm ơi:<
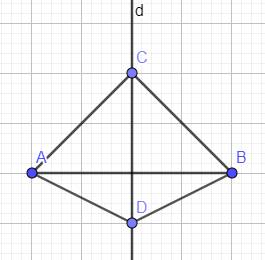
vẽ đoạn thẳng AB=4cm.vẽ đường thẳng d là đường trung trực của AB .Lấy điểm C,D thuộc d(C,D không thuộc AB). chứng minh ΔACD=ΔBCD
Có `C in d` và `d` là trung trực của `AB=>AC=BC`
`D in d` và `d` là trung trực của `AB=>AD=BD`
Xét `Delta ACD` và `Delta BCD` có :
`{:(AC=BC(cmt)),(CD-chung),(AD=BD(cmt)):}}`
`=>Delta ACD=Delta BCD(c.c.c)(đpcm)`
Đúng 1
Bình luận (0)
Câu 22: Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm K sao cho AK AB. a) Chứng minh rằng ∆CBK là tam giác cân. b) Gọi N là trung điểm của CK, đường thẳng qua K và song song với BC cắt đường thẳng BM tại H. Chứng minh rằng BC KE và BC + BK BE. c) Gọi G là giao điểm của AE và KM. Chứng minh rằng BC 6GM.Giaỉ theo cách lớp 7 nhéCâu c thôi nhé
Đọc tiếp
Câu 22: Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm K sao cho AK = AB.
a) Chứng minh rằng ∆CBK là tam giác cân.
b) Gọi N là trung điểm của CK, đường thẳng qua K và song song với BC cắt đường thẳng BM tại H. Chứng minh rằng BC = KE và BC + BK > BE.
c) Gọi G là giao điểm của AE và KM. Chứng minh rằng BC = 6GM.
Giaỉ theo cách lớp 7 nhé
Câu c thôi nhé
a: Xet ΔCBK có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBK cân tạiC
b: Sửa đề: M là trung điểm của KC
Xét ΔMEK và ΔMBC có
góc MKE=góc MCB
MK=MC
góc KME=góc BMC
=>ΔMEK=ΔMBC
=>EK=BC
c: Xét ΔEKB có
KM,EA là trung tuyến
KM cắt EA tại G
=>G là trọng tâm
=>GM=1/3MK=1/3MC=1/6CK=1/6BC
Đúng 2
Bình luận (0)