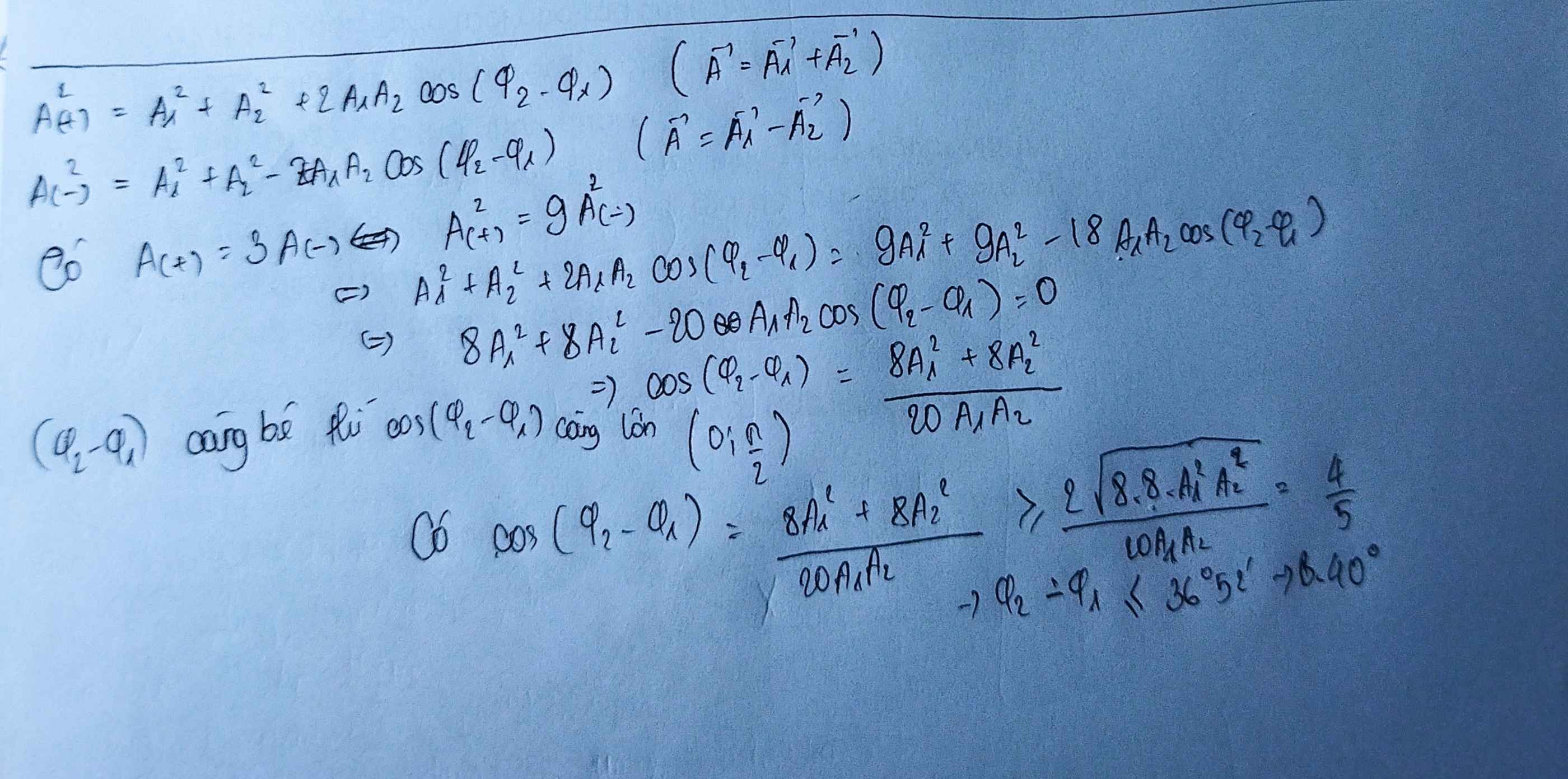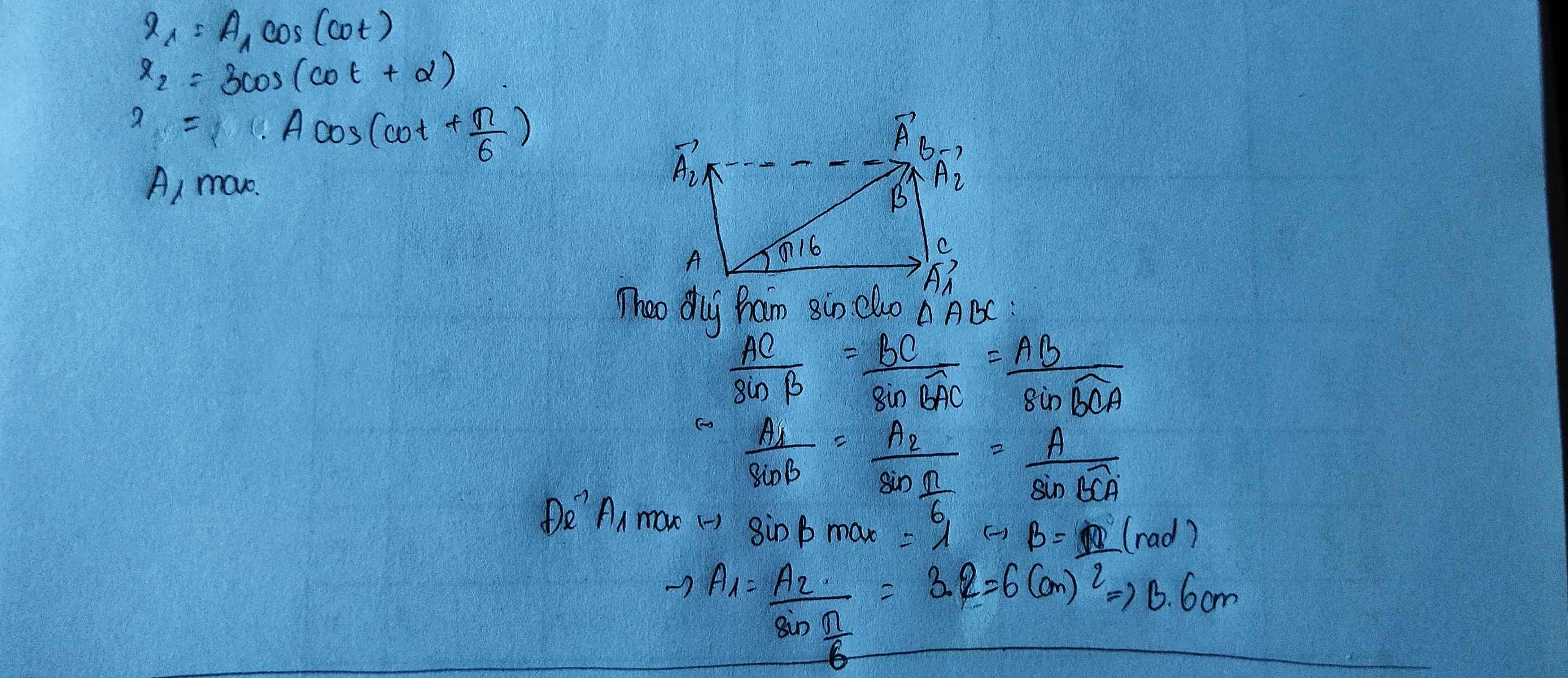Có phương trình tổng hợp 2 dao động điều hòa sau : x1= 5 cos (omêga t - π/2) x2= 5√3 cos ( omêga t + π/4) Tìm phương trình dao động tổng hợp của hai dao động trên
Bài 5. Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen

hãy cứu rỗi một đứa mất gốc lí như tớ huhu
hai dđđh cùng phương có phương trình x1 4cos(pi.t-pi/6)cm và x2 4cos(pi.t-pi/2)cm dao động tổng hợp của 2 giao động này có biên độ là ?hai dđđh cùng phương có phương trình x1 4cos100pi.t cm và x2 3cos(100pi.t+pi/2)cm dao động tổng hợp của 2 giao động này có biên độ là ?một vật thực hiện đồng thời 2 dđđh cùng phương theo các phương trình x1 -4sin(pi.t)cm và x2 4cawn 3 cos(pi.t)cm phương trình của dao động tổng hợp là
Đọc tiếp
hai dđđh cùng phương có phương trình x1 = 4cos(pi.t-pi/6)cm và x2 = 4cos(pi.t-pi/2)cm dao động tổng hợp của 2 giao động này có biên độ là ?
hai dđđh cùng phương có phương trình x1 4cos100pi.t cm và x2 = 3cos(100pi.t+pi/2)cm dao động tổng hợp của 2 giao động này có biên độ là ?
một vật thực hiện đồng thời 2 dđđh cùng phương theo các phương trình x1 =-4sin(pi.t)cm và x2 = 4cawn 3 cos(pi.t)cm phương trình của dao động tổng hợp là
một vật tham gia đồng thời hai dao điều hoà cùng phương có phương trình lần lượt là x1=6cos(wt) cm x2 = 6 căn 3 cos(wt+pi/2) pha ban đầu của dao động tổng hợp là
Hai vật dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là x1=A1cos(ωt + φ1) và x2 = A2cos(ωt + φ2). Gọi x(+) = x1 + x2 và x(-) = x1 - x2. Biết rằng biên độ dao động của x(+) gấp 3 lần biên độ dao động của x(-). Độ lệch pha cực đại giữa x1 và x2 gần nhất với giá trị nào sau đây ?
A. 50° B. 40° C. 30° D. 60°
Một vật thực hiện đồng thời 3 dao động điều hòa cùng phương cùng tần số có
phương trình là x1, x2, x3. Biết x12 = 6cos(πt + π/6) cm; x23 = 6cos(πt + 2π/3) cm;
x13 = 6√2cos(πt + 5π/12) cm. Tính x biết x2 = x12 + x32
A. 6√2 cm B. 12 cm C. 24 cm D. 6√3 cm
Ai biết giúp mình với!!
Câu 1: Một chất điểm tham gia đồng thời hai dao động cùng phương. Phương trình ly độ của
các dao động thành phần và dao động tổng hợp lần lượt là x1 = A1cos(ωt) cm; x2 = 3cos(ωt +
α) cm; và x = Acos(ωt+ π/6) cm. Biên độ dao động A1 có giá trị lớn nhất là
A. 9 cm. B. 6 cm. C. 8 cm. D. 12 cm.
một vật thực hiện hai dao động điều hòa cùng phương cùng tần số có biên độ và pha ban đầu lần lượt là: A1,A2,f1=-π/3 rad,f2=π/2rad dao động tổng hợp có biên độ là 9 cm. khi A2 có giá trị cực đại thì A1 và A2 có giá trị là
Xem chi tiết

\(\overrightarrow{A}=\overrightarrow{A_1}+\overrightarrow{A_2}\)
Định lý hàm sin: \(\dfrac{A}{\sin\dfrac{\pi}{6}}=\dfrac{A_2}{\sin\alpha}=\dfrac{A_1}{\sin\beta}\)
\(A_2\left(max\right)\Rightarrow\sin\alpha_{max}=1\Rightarrow\left\{{}\begin{matrix}A_2=\dfrac{9}{\dfrac{1}{2}}=18\left(cm\right)\\\alpha=\dfrac{\pi}{2}\left(rad\right)\end{matrix}\right.\)
\(\Rightarrow\beta=\pi-\dfrac{\pi}{6}-\dfrac{\pi}{2}=\dfrac{\pi}{3}\left(rad\right)\Rightarrow A_1=18.\sin\dfrac{\pi}{3}=9\sqrt{3}\left(cm\right)\)
Đúng 2
Bình luận (0)
Vật dao động điều hòa, chọn gốc tọa độ tại vị trí cân bằng gốc thời gian khi vật ở biên dương. Phương trình dao động của vật là
Mọi người giúp e vs ạ
Hỏi chấm? :) Ko cho dữ kiện để tính omega thì tính kiểu gì bạn ei
Đúng 0
Bình luận (0)