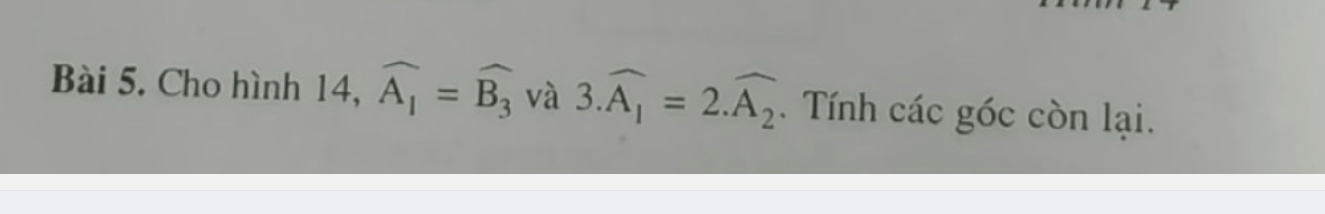
Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng

vì m//n

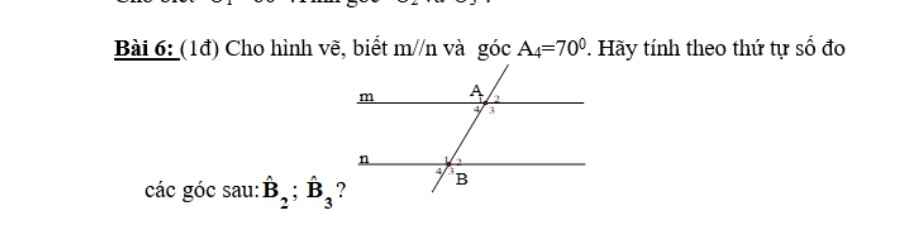
-->\(\widehat B_2=\widehat A_4(2 góc so le trong) \) 

mà\(\widehat A_4\)=70\(^o\)

-->\(\widehat B_2\)=70\(^o\)

ta có \(\widehat B _2+\widehat B_3=180^o\)

-->\(\widehat B_3=110^o\)

Hình vuông ABCD đâu?

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

Gọi Ax đối AB

\(\Rightarrow\widehat{xAE}=180^0-\widehat{BAE}=80^0\left(kề.bù\right)\\ \Rightarrow\widehat{xAC}=\widehat{EAC}-\widehat{xAE}=120^0-80^0=40^0\\ \Rightarrow\widehat{xAC}+\widehat{ACD}=40^0+140^0=180^0\)

Mà 2 góc này ở vị trí trong cùng phía nên Ax//CD

Mà Ax đối AB nên AB//CD

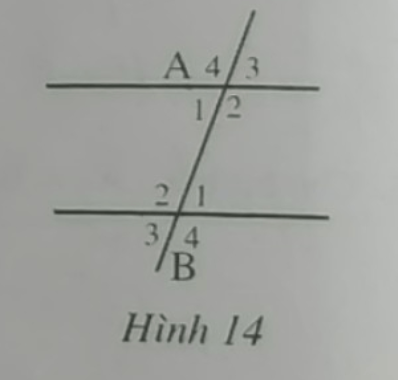
Ta có \(\widehat{A_1}=\widehat{B_3}\) mà 2 góc này ở vị trí đồng vị nên a//b

Ta có \(3\widehat{A_1}=2\widehat{A_2}\Rightarrow\dfrac{\widehat{A_1}}{2}=\dfrac{\widehat{A_2}}{3}\)

Mà \(\widehat{A_1}+\widehat{A_2}=180^0\left(kề.bù\right)\)

Áp dụng t/c dtsbn:

\(\dfrac{\widehat{A_1}}{2}=\dfrac{\widehat{A_2}}{3}=\dfrac{\widehat{A_1}+\widehat{A_2}}{2+3}=\dfrac{180^0}{5}=36^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=72^0\\\widehat{A_2}=108^0\end{matrix}\right.\)

Ta có \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}=72^0\\\widehat{A_2}=\widehat{A_4}=108^0\end{matrix}\right.\left(đối.đỉnh\right)\)

Ta có a//b nên \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{B_1}=72^0\\\widehat{A_2}=\widehat{B_2}=108^0\end{matrix}\right.\left(so.le.trong\right);\left\{{}\begin{matrix}\widehat{A_1}=\widehat{B_3}=72^0\\\widehat{A_2}=\widehat{B_4}=108^0\end{matrix}\right.\left(đồng.vị\right)\)

nhanh lên nhé mình cần gấp!

Cái thang, mặt bàn