Cho phương trình \({x^2} + 2x + c = 0\). Điều kiện của c để phương trình có 2 nghiệm phân biệt là:
A. \(c < 1\)
B. \(c > 1\)
C. \(c \le 1\)
D. \(c \ge 1\)
Cho phương trình \({x^2} + 2x + c = 0\). Điều kiện của c để phương trình có 2 nghiệm phân biệt là:
A. \(c < 1\)
B. \(c > 1\)
C. \(c \le 1\)
D. \(c \ge 1\)
Giả sử đồ thị của hàm số \(y = a{x^2}(a \ne 0)\) là parabol ở Hình 9. Giá trị của a bằng:
A. 2
B. \( - 2\)
C. \(\frac{1}{2}\)
D. \(\frac{{ - 1}}{2}\)
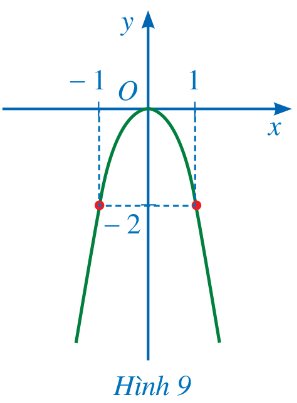
Vì điểm \(\left( {1; - 2} \right)\) thuộc đồ thị hàm số, nên thay \(x = 1;y = - 2\) vào \(y = a{x^2}\), ta được:
\(\begin{array}{l} - 2 = a{.1^2}\\a = - 2(TM)\end{array}\)
Chọn đáp án B.
Trả lời bởi datcoderCho hàm số \(y = \frac{{ - 2}}{3}{x^2}\).
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

b) Dựa vào bảng trên, vẽ đồ thị của hàm số.
a)
| \(x\) | \(-3\) | \(-1\) | \(0\) | \(1\) | \(3\) |
| \(y=-\dfrac{2}{3}x^2\) | \(-6\) | \(-\dfrac{2}{3}\) | \(0\) | \(-\dfrac{2}{3}\) | \(-6\) |
b)
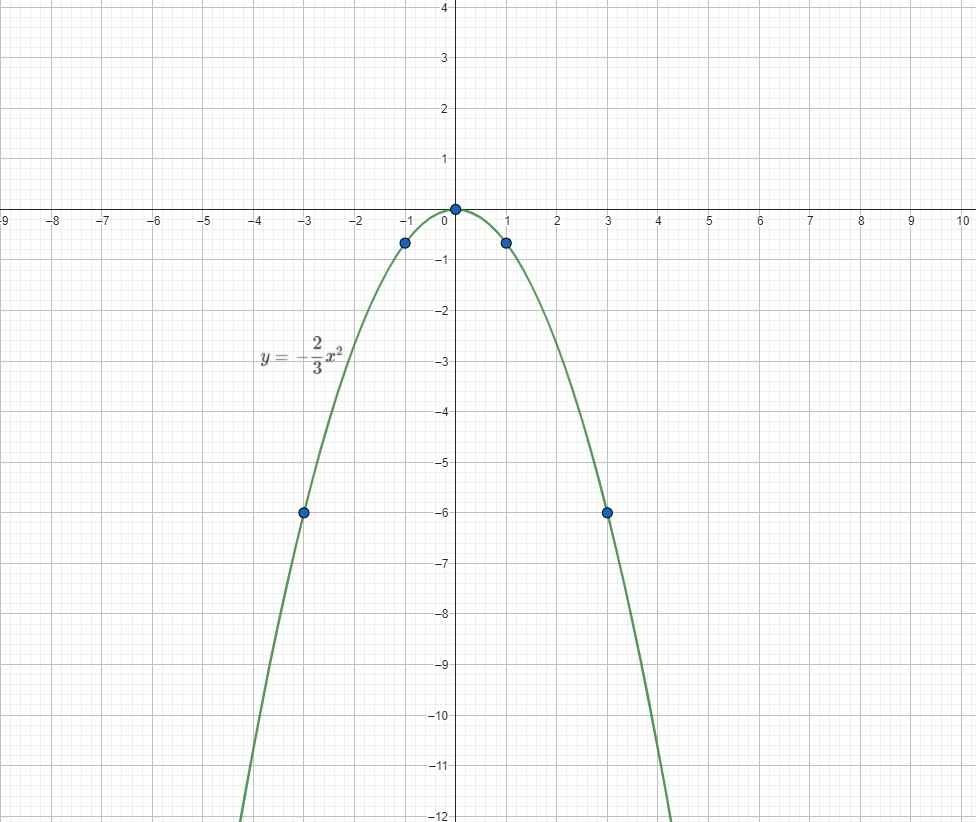
Trả lời bởi Nguyễn Tuấn Tú
Trên mặt phẳng tọa độ Oxy, đường parabol ở Hình 10 biểu diễn đồ thị của hàm số \(y = a{x^2}\).
a) Tìm hệ số a.
b) Tìm điểm thuộc đồ thị hàm số có hoành độ bằng 3.
c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 4.
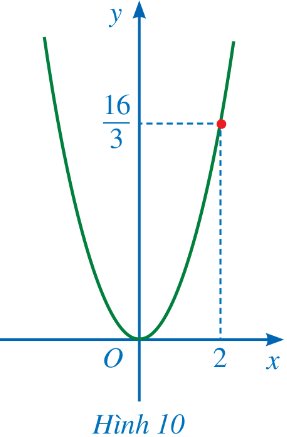
a) Vì điểm \(\left( {2;\frac{{16}}{3}} \right)\) thuộc đồ thị hàm số, nên thay \(x = 2;y = \frac{{16}}{3}\) vào \(y = a{x^2}\), ta được:
\(\begin{array}{l}\frac{{16}}{3} = a{.2^2}\\a = \frac{4}{3}\end{array}\)
Vậy \(a = \frac{4}{3}\)
b) Với \(a = \frac{4}{3}\) hàm số trở thành \(y = \frac{4}{3}{x^2}.\)
Điểm thuộc đồ thị hàm số có hoành độ bằng 3 nên \(x = 3,\) ta có:
\(\begin{array}{l}y = \frac{4}{3}{x^2}\\y = \frac{4}{3}{.3^2} = 12.\end{array}\)
Vậy điểm cần tìm là \(\left( {3;12} \right)\).
c) Điểm thuộc đồ thị hàm số có tung độ bằng 4 nên \(y = 4.\) Ta có:
\(\begin{array}{l}y = \frac{4}{3}{x^2}\\4 = \frac{4}{3}{x^2}\end{array}\)
\(x = \pm \sqrt 3 \)
Vậy điểm cần tìm là \(\left( {\sqrt 3 ;4} \right),\left( { - \sqrt 3 ;4} \right).\)
Trả lời bởi datcoderGiải các phương trình:
a) \(3{x^2} - 2x - 4 = 0\)
b) \(9{x^2} - 24x + 16 = 0\)
c) \(2{x^2} + x + \sqrt 2 = 0\)
a) Phương trình có các hệ số: \(a = 3;b = - 2;c = - 4.\) Do \(b = - 2\) nên \(b' = - 1.\)
\(\Delta ' = {( - 1)^2} - 3.( - 4) = 13 > 0\)
Phương trình có 2 nghiệm phân biệt là:
\({x_1} = \frac{{ - \left( { - 1} \right) + \sqrt {13} }}{3} = \frac{{1 + \sqrt {13} }}{3};{x_2} = \frac{{ - \left( { - 1} \right) - \sqrt {13} }}{3} = \frac{{1 - \sqrt {13} }}{3}.\)
b) Phương trình có các hệ số: \(a = 9;b = - 24;c = 16.\) Do \(b = - 24\) nên \(b' = - 12.\)
\(\Delta ' = {( - 12)^2} - 9.16 = 0\)
Phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{ - \left( { - 12} \right)}}{9} = \frac{4}{3}.\)
c) Phương trình có các hệ số: \(a = 2;b = 1;c = \sqrt 2 .\)
\(\Delta ' = {1^2} - 4.2.\sqrt 2 = 1 - 8\sqrt 2 < 0\)
Vậy phương trình vô nghiệm.
Trả lời bởi datcoderKhông tính \(\Delta \), hãy giải các phương trình:
a) \({x^2} - 3x + 2 = 0\)
b) \( - 3{x^2} + 5x + 8 = 0\)
c) \(\frac{1}{3}{x^2} + \frac{1}{6}x - \frac{1}{2} = 0\)
a)
\(x^2-3x+2=0\\
\Leftrightarrow\left(x^2-2x\right)-\left(x-2\right)=0\\
\Leftrightarrow x\left(x-2\right)-\left(x-2\right)=0\\
\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\\
\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
b)
\(-3x^2+5x+8=0\\
\Leftrightarrow-\left(3x^2+3x\right)+\left(8x+8\right)=0\\
\Leftrightarrow-3x\left(x+1\right)+8\left(x+1\right)=0\\
\Leftrightarrow\left(x+1\right)\left(8-3x\right)=0\\
\Leftrightarrow\left[{}\begin{matrix}x+1=0\\8-3x=0\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=-1\\3x=8\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{8}{3}\end{matrix}\right.\)
c)
\(\dfrac{1}{3}x^2+\dfrac{1}{6}x-\dfrac{1}{2}=0\\
\Leftrightarrow\dfrac{2x^2}{6}+\dfrac{x}{6}-\dfrac{3}{6}=0\\
\Leftrightarrow\dfrac{2x^2+x-3}{6}=0\\
\Leftrightarrow2x^2+x-3=0\\
\Leftrightarrow\left(2x^2-2x\right)+\left(3x-3\right)=0\\
\Leftrightarrow2x\left(x-1\right)+3\left(x-1\right)=0\\
\Leftrightarrow\left(2x+3\right)\left(x-1\right)=0\\
\Leftrightarrow\left[{}\begin{matrix}2x+3=0\\x-1=0\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}2x=-3\\x=1\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=1\end{matrix}\right.\)
Vậy...
Tìm hai số biết tổng của chúng bằng \(4\sqrt 2 \) và tích của chúng bằng 6.
a) Hai số cần tìm là nghiệm của phương trình: \({x^2} - 4\sqrt 2 x + 6 = 0\).
Phương trình có các hệ số: \(a = 1;b = - 4\sqrt 2 ;c = 6.\) Do \(b = - 4\sqrt 2 \) nên \(b' = - 2\sqrt 2 .\)
\(\Delta ' = {( - 2\sqrt 2 )^2} - 1.6 = 2 > 0\)
Phương trình có 2 nghiệm phân biệt là: \({x_1} = \frac{{ - \left( { - 2\sqrt 2 } \right) + \sqrt 2 }}{1} = 3\sqrt 2 ;{x_2} = \frac{{ - \left( { - 2\sqrt 2 } \right) - \sqrt 2 }}{1} = \sqrt 2 .\)
Vậy hai số cần tìm là \(3\sqrt 2 ;\sqrt 2 .\)
Trả lời bởi datcoderGiải thích vì sao nếu phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},{x_2}\) thì \(a{x^2} + bx + c = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\).
Áp dụng phân tích các đa thức sau thành nhân tử:
a) \({x^2} - 2x - 3\)
b) \(3{x^2} + 5x - 2\)
Do phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},{x_2}\) nên áp dụng định lý Viète, ta có:
\({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}.{x_2} = \frac{c}{a}\)
Ta lại có:
\(\begin{array}{l}VT = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) = a\left( {{x^2} - x.{x_2} - x.{x_1} + {x_1}.{x_2}} \right)\\ = a\left[ {{x^2} - x\left( {{x_1} + {x_2}} \right) + {x_1}.{x_2}} \right]\\ = a\left[ {{x^2} - x.\frac{{ - b}}{a} + \frac{c}{a}} \right]\\ = a\left( {{x^2} + \frac{b}{a}x + \frac{c}{a}} \right)\\ = a{x^2} + bx + c\\ = VP(dpcm)\end{array}\)
a) Ta có \(a - b + c = 0\) nên phương trình có hai nghiệm \({x_1} = - 1;{x_2} = 3\).
Vậy \({x^2} - 2x - 3 = \left( {x + 1} \right)\left( {x - 3} \right)\)
b) Ta có: \(\Delta = {5^2} - 4.3.\left( { - 2} \right) = 49 > 0\)
Phương trình có hai nghiệm là \({x_1} = \frac{{ - 5 + \sqrt {49} }}{{2.3}} = \frac{2}{6} = \frac{1}{3}\); \({x_2} = \frac{{ - 5 - \sqrt {49} }}{{2.3}} = \frac{{ - 12}}{6} = - 2\).
Vậy \(3{x^2} + 5x - 2 = 3.\left( {x - \frac{1}{3}} \right)\left( {x + 2} \right)\)
Trả lời bởi datcoderMột chiếc áo có giá niêm yết là 120 000 đồng. Để thanh lí chiếc áo, đầu tiên người ta giảm giá x% so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá x% so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn 76800 đồng. Tìm x.
Điều kiện: \(0 < x < 100.\)
Sau khi giảm giá lần đầu tiên, giá của chiếc áo là:
\(120000 - x\% .120000 = 120000 - 1200x\) (đồng).
Sau khi giảm giá lần thứ 2, giá của chiếc áo là:
\(120000 - 1200x - x\% (120000 - 1200x) \)
\(= 12{x^2} - 2400x + 120000\) (đồng).
Vì giá của chiếc áo còn 76800 đồng nên ta có phương trình:
\(\begin{array}{l}12{x^2} - 2400x + 120000 = 76800\\{x^2} - 200x + 3600 = 0\end{array}\)
Phương trình có các hệ số: \(a = 1;b = - 200;c = 3600.\) Do \(b = - 200\) nên \(b' = - 100.\)
\(\Delta ' = {\left( { - 100} \right)^2} - 1.3600 = 6400 > 0\)
Phương trình có 2 nghiệm phân biệt là: \({x_1} = \frac{{ - \left( { - 100} \right) + \sqrt {6400} }}{1} = 180;{x_2} = \frac{{ - \left( { - 100} \right) - \sqrt {6400} }}{1} = 20.\)
Vì \(0 < x < 100\) nên \(x = 20.\)
Vậy \(x = 20.\)
Trả lời bởi datcoderMột công ty sản xuất các khay có dạng hình hộp chữ nhật để trồng rau trong chung cư ở các thành phố. Biết diện tích mặt đáy của khay đó là 2 496 cm2 và chu vi mặt đáy của khay đó là 220 cm. Tìm các kích thước mặt đáy của khay đó.
Gọi 2 kích thước mặt đáy của khay hình chữ nhật là \(x_1; x_2\) (cm) (x_1;x_2 > 0)
Theo đề bài, ta có:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{220}}{2} = 110\\{x_1}.{x_2} = 2496\end{array} \right.\)
Khi đó \(x_1; x_2\) là hai nghiệm của phương trình:
\(x^2 - 110x + 2496 = 0\), \(b' = \frac{-110}{2} = -55\)
Ta có: \(\Delta ' = (-55)^2 - 1.2496 = 529 > 0\)
Phương trình có hai nghiệm phân biệt \(x_1 = \frac{ 55 + \sqrt{529}}{1} = 78\) (TM); \(x_1 = \frac{ 55 - \sqrt{529}}{1} = 32\) (TM)
Vì 78 > 32 nên chiều dài là 78cm, chiều rộng là 32cm.
Vậy chiều dài mặt đáy của khay là 78cm, chiều rộng mặt đáy của khay 32cm.
Trả lời bởi datcoder
\(\Delta ' = b{'^2} - ac = {1^1} - 1.c = 1 - c\)
Để phương trình có 2 nghiệm phân biệt thì \(\Delta ' = 1 - c > 0\) do đó \(c < 1\)
Chọn đáp án A.
Trả lời bởi datcoder