Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB ta được một hình trụ có bán kính bằng độ dài đoạn thẳng
A. AB. B. CD. C. AD. D. AC.
Cho tam giác ABC vuông tại A có AB = 4 cm, BC = 5 cm. Khi quay tam giác ABC một vòng quanh AC ta được một hình nón có chiều cao bằng
A. 4 cm. B. 3 cm. C. 5 cm. D. 9 cm.
Đ/A là câu A. 4cm
Trả lời bởi RAVG416Diện tích mặt cầu có đường kính 10 cm là
A. 10π cm2. B. 400π cm2. C. 50π cm2. D. 100π cm2.
Đ/A là câu D.100π \(cm^2\)
Trả lời bởi RAVG416Cho hình nón có bán kính đáy R = 2 cm, độ dài đường sinh ℓ = 5 cm. Diện tích xung quanh của hình nón đã cho bằng
A. \(\dfrac{10\pi}{3}\) cm2.
B. \(\dfrac{50\pi}{3}\) cm2.
C. 20π cm2.
D. 10π cm2.
Diện tích xung quanh hình nón là:
\(S = \pi .2.5 = 10\pi \left( {c{m^2}} \right)\)
Chọn D
Trả lời bởi datcoderMột mặt phẳng đi qua tâm hình cầu, cắt hình cầu theo một hình tròn có diện tích 9π cm2. Thể tích của hình cầu bằng
A. 972π cm3. B. 36π cm3.
C. 6π cm3. D. 81π cm3.
Vì hình tròn đi qua tâm hình cầu có diện tích \(9\pi \;c{m^2}\) nên ta có: \(\pi {R^2} = 9\pi \) nên bán kính hình tròn đi qua tâm là \(R = 3\). Vì bán kính hình cầu bằng bán kính đường tròn đi qua tâm hình cầu nên \(R = 3\).
Thể tích hình cầu là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\)
Chọn B
Trả lời bởi datcoderCho hình trụ có bán kính đáy bằng 20 cm, chiều cao bằng 30 cm.
a) Tính diện tích xung quanh của hình trụ.
b) Tính thể tích của hình trụ.
a) Diện tích xung quanh của hình trụ là
2π.20.30=1200π≃3769,9 (\(cm^2\))
b) Thể tích của hình trụ là
π.\(20^2\).30=12000π≃37699,1 (\(cm^3\))
Trả lời bởi RAVG416
Cho hình nón có bán kính đáy bằng 9 cm, độ dài đường sinh bằng 15 cm (H.10.34).
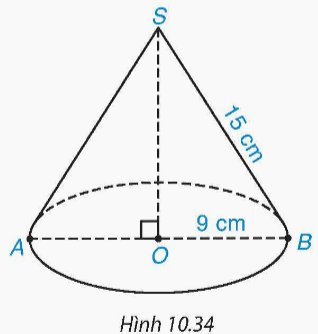
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.
Xét hình nón có đường sinh \(SB = 15cm\) và bán kính đáy \(OB = 9cm\).
Tam giác SOB vuông tại O nên \(S{O^2} + O{B^2} = S{B^2}\)
\({9^2} + S{O^2} = {15^2}\)
\(SO = 12cm\)
a) Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi .OB.SB = 9.15.\pi = 135\pi \left( {c{m^2}} \right)\).
b) Thể tích của hình nón là:
\(V = \frac{1}{3}\pi .O{B^2}.SO = \frac{1}{3}{.9^2}.12.\pi = 324\pi \left( {c{m^3}} \right)\).
c) Diện tích đáy hình nón là:
\({S_{đáy}} = \pi .O{B^2} = {9^2}\pi = 81\pi \left( {c{m^2}} \right)\).
Diện tích toàn phần của hình nón là:
\(S = {S_{xq}} + {S_{đáy}} = 135\pi + 81\pi = 216\pi \left( {c{m^2}} \right)\).
Trả lời bởi datcoderQuả bóng rổ sử dụng trong thi đấu có dạng hình cầu với đường kính bằng 24 cm (H.10.35). Hãy tính:
a) Diện tích bề mặt quả bóng.
b) Thể tích của quả bóng.
Bán kính quả bóng là: \(R = 24:2 = 12\left( {cm} \right)\)
a) Diện tích bề mặt quả bóng là:
\(V = 4\pi {R^2} = 4\pi {.12^2} = 576\pi \left( {c{m^2}} \right)\).
b) Thể tích của quả bóng là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.12^3} = 2304\pi \left( {c{m^3}} \right)\).
Trả lời bởi datcoderĐèn trời có dạng hình trụ không có một đáy với đường kính đáy bằng 0,8 m và thân đèn cao 1 m (H.10.36). Tính diện tích giấy đèn bên ngoài đèn trời (coi các mép dán không đáng kể).
Bán kính đáy đèn trời là: \(R = \frac{{0,8}}{2} = 0,4\left( m \right)\).
Diện tích xung quanh của đèn trời là:
\({S_{xq}} = 2\pi Rh = 2\pi .0,4.1 = 0,8\pi \left( {{m^2}} \right)\).
Diện tích đáy hình trụ là:
\({S_{đáy}} = \pi {R^2} = \pi .0,{4^2} = 0,16\pi \left( {{m^2}} \right)\).
Diện tích giấy dán bên ngoài đèn trời:
\(S = {S_{đáy}} + {S_{xq}} = 0,16\pi + 0,8\pi = 0,96\pi \left( {{m^2}} \right)\).
Trả lời bởi datcoderCác hình dưới đây (H.10.37) được tạo thành từ các nửa hình cầu, hình trụ và hình nón (có cùng bán kính đáy). Tính thể tích của các hình đó theo kích thước đã cho.
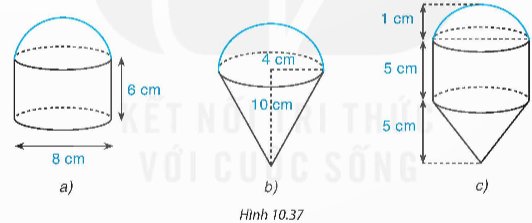
Hình a: Bán kính đường tròn đáy là: \(R = \frac{8}{2} = 4cm\).
Thể tích của hình trụ có bán kính 4cm, chiều cao 6cm là:
\({V_1} = \pi {.4^2}.6 = 96\pi \left( {c{m^3}} \right)\).
Thể tích nửa hình cầu có bán kính 4cm là:
\({V_2} = \frac{1}{2}.\frac{4}{3}\pi {.4^3} = \frac{{128}}{3}\pi \left( {c{m^3}} \right)\).
Thể tích hình a là:
\(V = {V_1} + {V_2} = 96\pi + \frac{{128\pi }}{3} = \frac{{416\pi }}{3}\left( {c{m^3}} \right)\).
Hình b: Thể tích của hình nón có bán kính đáy 4cm, chiều cao 10cm là:
\({V_1} = \frac{1}{3}\pi {.4^2}.10 = \frac{{160\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích nửa hình cầu có bán kính 4cm là:
\({V_2} = \frac{1}{2}.\frac{4}{3}\pi {.4^3} = \frac{{128\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích hình b là:
\(V = {V_1} + {V_2} = \frac{{160\pi }}{3} + \frac{{128\pi }}{3} = 96\pi \left( {c{m^3}} \right)\).
Hình c: Thể tích của hình trụ có bán kính đáy 1cm, chiều cao 5cm là:
\({V_1} = \pi {.1^2}.5 = 5\pi \left( {c{m^3}} \right)\).
Thể tích của hình nón có bán kính đáy 1cm, chiều cao 5cm là:
\({V_2} = \frac{1}{3}\pi {.1^2}.5 = \frac{{5\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích nửa hình cầu có bán kính 1cm là:
\({V_3} = \frac{1}{2}.\frac{4}{3}\pi {.1^3} = \frac{{2\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích hình c là:
\(V = {V_1} + {V_2} + {V_3} = 5\pi + \frac{{5\pi }}{3} + \frac{{2\pi }}{3} = \frac{{22\pi }}{3}\left( {c{m^3}} \right)\).
Trả lời bởi datcoder
Đ/A là câu C.AD
Trả lời bởi RAVG416