Trong hoạt động mở đầu:
a) Các tia sáng \(AA',BB',DD'\) có song song với nhau hay không?
b) Nêu cách xác định bóng \(C'\) của điểm \(C\) trên mặt đường.
Tìm phương chiếu, mặt phẳng chiếu của phép chiếu song song được mô tả trong Hình 2.
Tìm ảnh của hình hộp \(ABEF.DCGH\) qua phép chiếu song song được mô tả trong Hình 3.
Ảnh của hình hộp ABEF.DCGH qua phép chiếu song song được mô tả trong hình 3 là hình hộp A'B'E'F'.D'C'G'H'
Trả lời bởi Nguyễn Lê Phước ThịnhTrong Hình 4, xét phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa đường thẳng \(a\) và song song với phương chiếu.
a) Khi điểm \(M\) thay đổi trên đường thẳng \(a\) thì ảnh \(M'\) của nó thay đổi ở đâu?
b) Từ đó hãy chỉ ra ảnh của đường thẳng \(a\) qua phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\).
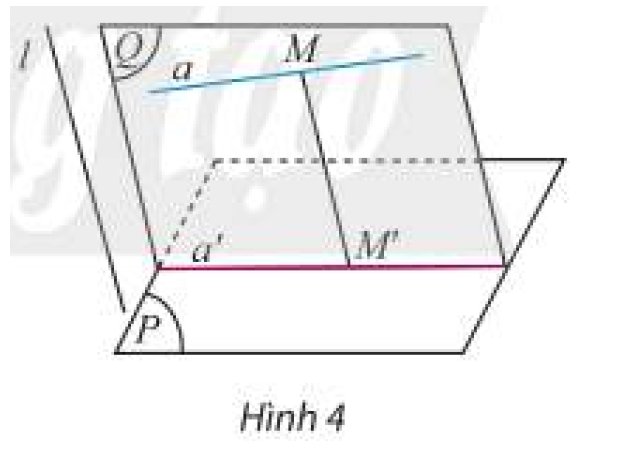
a: M' thay đổi trên a'
b: Ảnh của a qua phép chiếu theo phương l trên mp(P) là đường thẳng a'
Trả lời bởi Nguyễn Lê Phước ThịnhTrong Hình 5, xét phép chiếu theo phương \(l\) với mặt phẳng chiếu \(\left( P \right)\). Biết \(a\parallel b\) với \(a \subset \left( Q \right)\) và \(b \subset \left( R \right)\). Nêu nhận xét về vị trí tương đối của hình chiếu \(a',b'\) của \(a,b\) trong hai trường hợp: \(\left( Q \right)\parallel \left( R \right);\left( Q \right) \equiv \left( R \right)\).
Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = b'\end{array} \right\} \Rightarrow a'\parallel b'\)
Vậy nếu \(\left( Q \right)\parallel \left( R \right)\) thì \(a'\parallel b'\); nếu \(\left( Q \right) \equiv \left( R \right)\) thì \(a' \equiv b'\).
Trả lời bởi Quoc Tran Anh LeCho hình thang \(ABCD\) có đáy lớn \(AB\) và \(AB = 2CD\), hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\). Chứng minh rằng \(A'B'C'D'\) cũng là một hình thang và \(A'B' = 2C'D'\).
\(ABCD\) là hình thang có đáy lớn \(AB \Rightarrow AB\parallel CD\).
Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\) nên \(A'B'\parallel C'D'\). Vậy \(A'B'C'D'\) cũng là một hình thang.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà \(AB = 2CD,AB\parallel CD\) và \(A'B'\parallel C'D'\) nên \(A'B' = 2C'D'\).
Trả lời bởi Quoc Tran Anh LeCho \(G\) là trọng tâm tam giác \(ABC\), \(M\) là trung điểm \(BC\) và hình chiếu song song của tam giác \(ABC\) là tam giác \(A'B'C'\). Chứng minh rằng hình chiếu \(M'\) của \(M\) là trung điểm của \(B'C'\) và hình chiếu \(G'\) của \(G\) cũng là trọng tâm tam giác \(A'B'C'\).
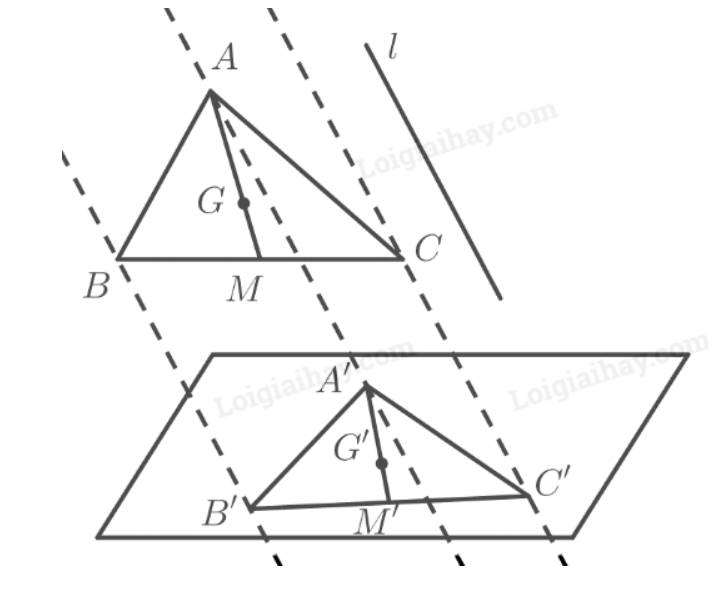
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).
Trả lời bởi Hà Quang MinhQuan sát Hình 7 và cho biết các tia nắng song song đã tạo ra hình chiếu của hình hộp như thế nào trên nền nhà.
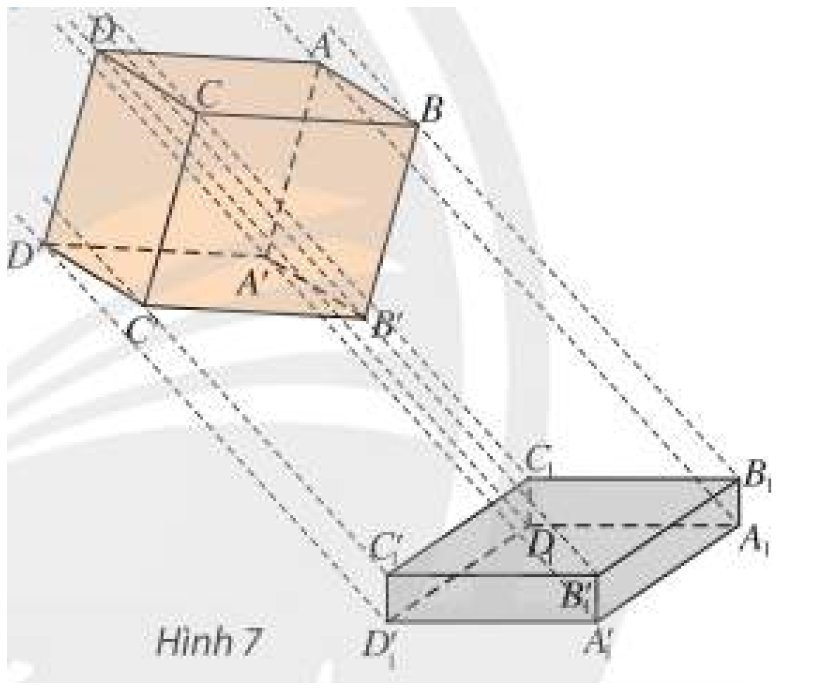
Các tia nắng song song đã tạo ra hình chiếu của hình hộp trên nền nhà là hình đa giác A1B1C1D1.A1'B1'C1'D1'.
Trả lời bởi Nguyễn Lê Phước ThịnhGọi tên các hình khối có hình biểu diễn là các hình trong Hình 10.
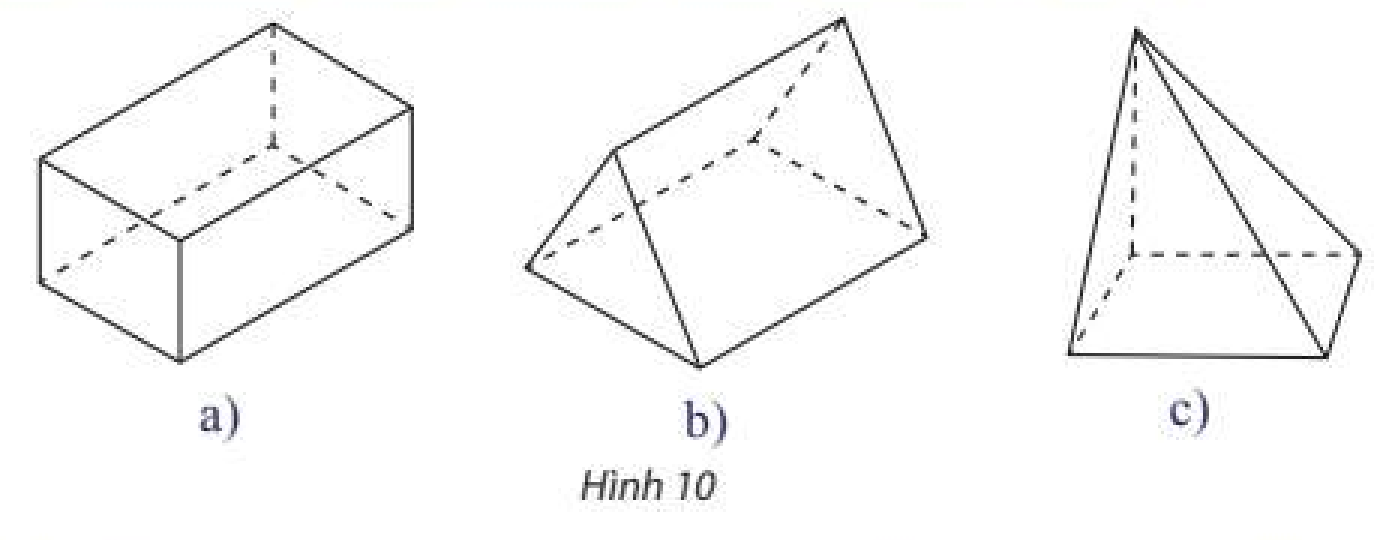
Vẽ hình biểu diễn của một hình chóp tam giác \(S.ABC\) đặt trên một hình lăng trụ tam giác \(ABC.A'B'C'\).
a) \(AA'\parallel BB'\parallel DD'\) vì cùng song song với đường thẳng \(l\).
b) Cách xác định bóng \(C'\) của điểm \(C\) trên mặt đường:
‒ Qua \(C\) dựng đường thẳng \(d\) song song với đường thẳng \(l\).
‒ Giao điểm của đường thẳng \(d\) với mặt đường chính là bóng \(C'\) của điểm \(C\).
Trả lời bởi Quoc Tran Anh Le