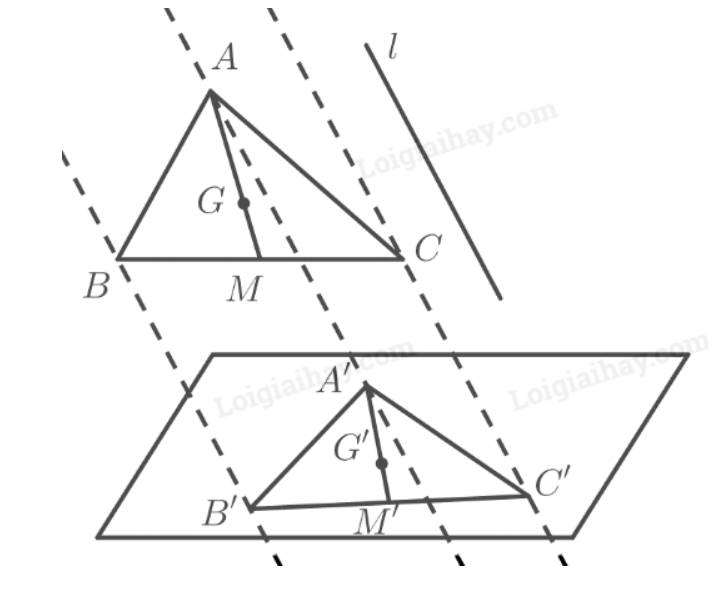
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).