Đề bài
Cho hình hộp ABCD.A’B’C’D‘. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA‘, C’D‘, AD‘. Chứng minh rằng:
a) NQ // A’D‘ và NQ=\(\dfrac{1}{2}\)A′D′
b) Tứ giác MNQC là hình bình hành
c) MN // (ACD‘)
d) (MNP) // (ACD‘)
Đề bài
Cho hình hộp ABCD.A’B’C’D‘. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA‘, C’D‘, AD‘. Chứng minh rằng:
a) NQ // A’D‘ và NQ=\(\dfrac{1}{2}\)A′D′
b) Tứ giác MNQC là hình bình hành
c) MN // (ACD‘)
d) (MNP) // (ACD‘)
Cho hình lăng trụ tam giác ABC.A’B’C‘. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B‘.
a) Chứng minh rằng EF // (BCC’B’)
b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC’B). Chứng minh rằng I là trung điểm đoạn thẳng CF.
a) Gọi H là trung điểm của BC
△ABC có: E là trung điểm của AC, H là trung điểm của BC
Suy ra: EH // AB
Mà AB // A'B'
Do đó: EH // A'B' hay EH // B'F (1)
Ta có: EH // AB nên \(\dfrac{EH}{AB}=\dfrac{EC}{AC}=\dfrac{1}{2}\)
Mà AB = A'B', B'F = \(\dfrac{1}{2}\) A'B'
Nên: EH = B'F (2)
(1)(2) suy ra: EHB'F là hình bình hành. Do đó: EF // B'H
Mà B'H thuộc (BCC'B')
Suy ra: EF // (BCC'B')
b) Gọi K là trung điểm AB
Dễ dàng chứng minh được FKBB' là hình bình hành
Ta có: FK // BB'
Mà BB' // CC'
Suy ra: FK // CC' (1)
Ta có: FK = BB', mà BB' = CC'
Do đó: FK = CC' (2)
(1)(2) suy ra FKCC' là hình bình hành
Mà hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường
Nên C'K cắt CF tại trung điểm của hai đường thẳng
mà C'K thuộc (AC'B) , CF cắt (AC'B) tại I (đề bài)
Do đó: I là trung điểm của CF.
Trả lời bởi Quoc Tran Anh LeHãy liệt kê các đường chéo của hình hộp ABCD.A’B’C’D’
A’C, AC’, D’B, DB’
Trả lời bởi Nguyễn Lê Phước ThịnhĐề bài
Cho hình hộp ABCD.A’B’C’D’.
a) Chứng minh rằng (ACB’) // (A’C’D’)
b) GọiG1,G2ần lượt là giao điểm của BD’ với các mặt phẳng (ACB’) và (A’C’D’).
Chứng minh rằngG1,G2
lần lượt là trọng tâm của hai tam giác ACB’ và A’C’D.
c) Chứng minh rằng BG1=G1G2=D′G2
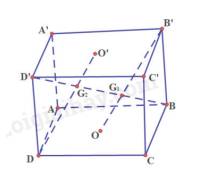
a) Ta có: AD // B’C’, AD = B’C’ nên ADC’B’ là hình bình hành
Suy ra AB’ // DC’ nên AB‘ // (A’C’D) (1)
Ta có: (ACC’A‘) là hình bình hành nên AC // A’C‘
Suy ra AC // (A’C’D‘) (2)
Mà AB‘, AC thuộc (ACB‘) (3)
Từ (1), (2), (3) suy ra (ACB‘) // (A‘C’D)
b) Gọi O, O’ lần lượt là tâm hình bình hành ABCD, A’B’C’D’
Trong (BDD’B’): B’O cắt BD’
Mà B’O thuộc (ACB’), BD’ cắt (ACB’) tại\({G_1}\)
Suy ra: B’O cắt BD’ tại\({G_1}\)
Tương tự, ta có: DO’ cắt BD’ tại\({G_2}\)
Ta có: tam giác \({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\) (do BD // B’D’)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{2}{3}\)
Do đó:\({G_1}\) là trọng tâm tam giác ACB’
Chứng minh tương tự ta có:\({G_2}\) là trọng tâm tam giác A’C’D
c) Ta có tam giác\({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \({G_1}B = \frac{1}{3}BD'(1)\)
Tương tự ta có:\(\frac{{{G_2}D'}}{{{G_2}B}} = \frac{{OD'}}{{DB}} = \frac{1}{2}\)
Nên \({G_2}D' = \frac{1}{3}{\rm{DD}}'(2)\)
Từ (1) và (2) suy ra\({G_1}B = {G_1}{G_2} = {G_2}D'\)
Trả lời bởi Quoc Tran Anh LeNêu nhận xét gì về hai mặt phẳng chứa hai mặt đối diện của hình hộp
Các mặt của hình hộp là các hình bình hành
Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau
Trả lời bởi Nguyễn Lê Phước ThịnhVẽ hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành
Từ định nghĩa hình lăng trụ, nhận xét đặc điểm các mặt bên, cạnh bên và hai mặt đáy của hình lăng trụ
Các cạnh bên của hình lăng trụ song song và bằng nhau
Các mặt bên của hình lăng trụ là các hình bình hành
Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau
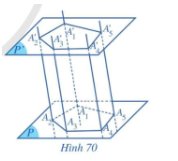
Trả lời bởi Nguyễn Lê Phước ThịnhCho hai mặt phẳng song song (P) và (P’).Trongmặtphẳng (P),chođagiác A1A2...An .Qua các đỉnh A1,A2,...,A vẽ các đường thẳng song song với nhau và cắt mặt phẳng (P) lần lượt tạiA1′,A2′,...,An′(Hình 70 minh họa cho trường hợp n = 5).
a) Các tứ giácA1A2A2′A1′,A2A3A3′A2′,...,AnA1A1′An′ là những hình gì?
b) Các cạnh tương ứng của hai đa giácA1A2...AnvàA1′A2.′..Ancó đặc điểm gì?
Cho một số ví dụ về những đồ dùng, vật thể trong thực tế có dạng hình lăng trụ
tòa nhà, hộp đựng phấn, viên gạch,...
Trả lời bởi Nguyễn Lê Phước ThịnhCho hình hộp ABCD.A’B’C’D’. Chứng minh rằng bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua một điểm.
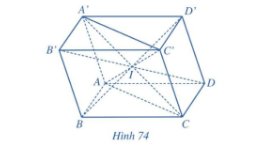
Gọi I là trung điểm của AC
Ta có: đường chéo hình hộp ABCD.A’B’C’D’ là A’C, AC’, D’B, DB’
Mà AC’,D’B thuộc (ABC’D’);
A’C,D’B thuộc (BCD’A’);
A’C,DB’ thuộc (CDA’B’)
AC’,DB’ thuộc (DAB’C’)
Do đó bốn mặt phẳng cùng đi qua điểm I
Trả lời bởi Nguyễn Lê Phước Thịnh
a) Ta có: N là trung điểm của AA’ nên \(\frac{{AN}}{{AA'}} = \frac{1}{2}\)
Q là trung điểm của AD’ nên \(\frac{{AQ}}{{AD'}} = \frac{1}{2}\)
Theo định lý Ta – let, ta có NQ // A’D’
Suy ra \(\frac{{NQ}}{{A'D'}} = \frac{{AN}}{{AA'}} = \frac{1}{2}\) nên\(NQ = \frac{1}{2}A'D'\)
b) Ta có: NQ // A’D’ mà A’D’ // BC nên NQ // BC hay NQ // MC (1)
Ta có \(NQ = \frac{1}{2}A'D'\) mà A’D’ = BC, \(MC = \frac{1}{2}BC\), nên NQ = MC (2)
Từ (1) và (2) suy ra MNQC là hình bình hành
c) Ta có: MNQC là hình bình hành nên MN // CQ
Mà CQ thuộc (ACD’)
Nên MN // (ACD’)
d) Gọi O là trung điểm của AC
Tam giác ACB có: O, M là trung điểm của AC, BC
Suy ra: OM // AB nên \(OM = \frac{1}{2}AB\)
Mà AB = C’D’, \(D'P = \frac{1}{2}C'D\),
Suy ra OM = D’P (1)
Ta có: OM // AB, AB // C’D’ nên OM // C’D‘ hay OM // D’P (2)
Từ (1) và (2) suy ra OMPD’ là hình bình hành. Do đó: MP // OD’
Mà OD’ thuộc (ACD’)
Suy ra: MP // (ACD’)
Mà MN thuộc (ACD’)
Do đó: (MNP) // (ACD’)
Trả lời bởi Quoc Tran Anh Le