Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D

Ta có: Tam giác ABC cân nên AB = AC

\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)

\( \Rightarrow AD\)là đường trung trực của BC.

Xét \(\Delta ABD\)và \(\Delta ACD\)có:

AB = AC (gt)

BD = CD (gt)

AD: cạnh chung

\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)

\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)

\( \Rightarrow \)AD là tia phân giác góc BAC.

Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.

b)

Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.

Tam giác ABC đều nên AB = BC = CA

Tam giác ABC cân tại A có AN là đường trung tuyến

\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)

Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC

Mà AN cắt BP tại G

\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC

\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất

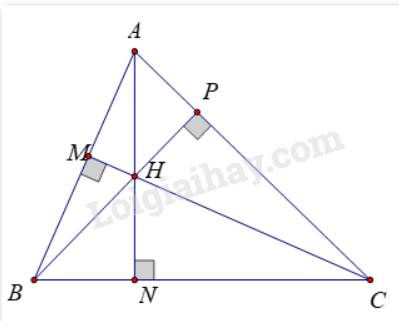
a)

Trong ΔABC ta có H là trực tâm nên:

AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M

Trong ΔAHB, ta có:

       HM ⊥ AB

       BN ⊥ AH

Mà MH cắt BN tại C

=> C là trực tâm của tam giác AHB.

Trong ΔHAC, ta có:

       HP ⊥ AC

       CN ⊥ AH

Mà HP cắt CN tại B

=> B là trực tâm của ΔHAC.

Trong ΔHBC, ta có:

       HN ⊥ BC

       BM ⊥ HC

Mà HN cắt BM tại A

=> A là trực tâm của tam giác HBC.

3 ngôi nhà không thẳng hàng nên tạo thành 1 tam giác, ta gọi là tam giác ABC.

Điểm khoan giếng cách đều 3 ngôi nhà khi và chỉ khi điểm khoan giếng là giao điểm của 3 đường trung trực của tam giác ABC.

Vậy, ta cần vẽ 2 đường trung trực của tam giác ABC, chúng cắt nhau tại đâu thì đó là điểm cần khoan giếng.

Ba đường cao AN, BP, CM cùng đi qua điểm H.

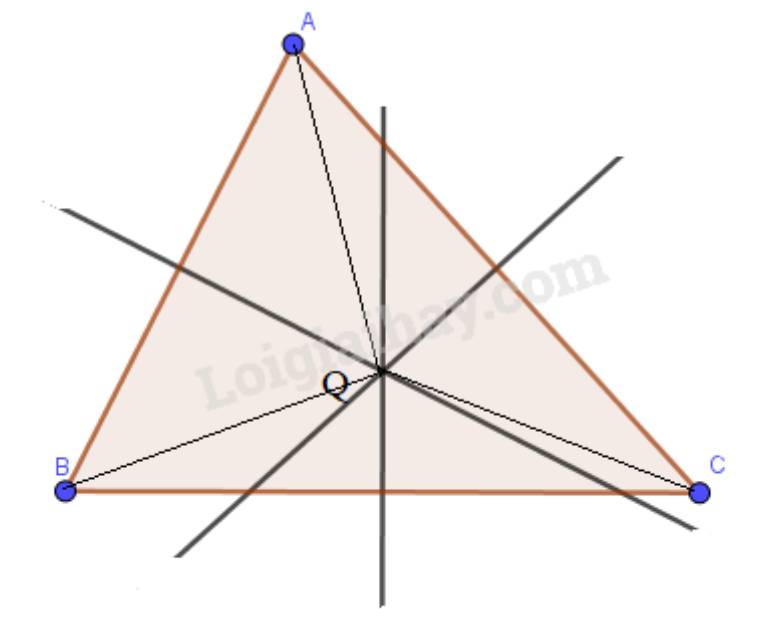
Vì Q cách đều 3 đỉnh của tam giác ABC nên QA=QB=QC

Vì QA=QB nên Q nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng).

Vì QA=QC nên Q nằm trên đường trung trực của đoạn thẳng AC (tính chất đường trung trực của đoạn thẳng).

Vì QB=QC nên Q nằm trên đường trung trực của đoạn thẳng BC (tính chất đường trung trực của đoạn thẳng).

Vậy Q là giao điểm của 3 đường trung trực của tam giác ABC.

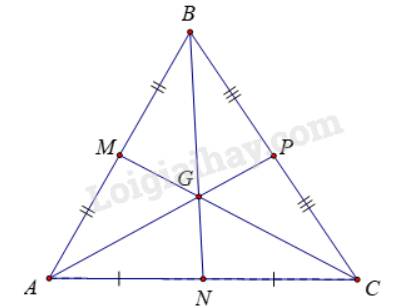
Tam giác ABC đều nên AB = BC = CA

Tam giác ABC cân tại B có BN là đường trung tuyến

\( \Rightarrow BN\)là đường trung trực của đoạn thẳng AC

Tam giác BAC cân tại A có AP là đường trung tuyến

\( \Rightarrow AP\)là đường trung trực của đoạn thẳng BC

Mà \(BN \cap AP = G\)

\( \Rightarrow G\)là giao điểm ba đường trung trực của tam giác ABC

\( \Rightarrow GA = GB = GC\).

Ba đường trung trực DP, DQ, DR cùng cắt nhau tại điểm D.

Mỗi tam giác có 3 đường trung trực.

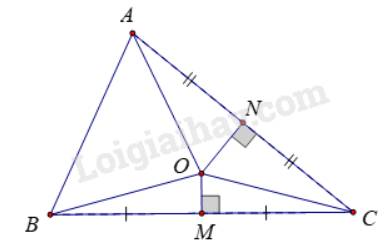
a)

Gọi M là trung điểm của BC, N là trung điểm AC.

Xét \(\Delta OBM\) và \(\Delta OCM\) có:

BM = CM (gt)                                                                                           

\(\widehat {OMB} = \widehat {OMC} = {90^0}\)

OM chung

\( \Rightarrow \Delta OBM = \Delta OCM\left( {c - g - c} \right)\)

\( \Rightarrow OB = OC\)(cạnh tương ứng)

Chứng minh tương tự: \(\Delta OAN = \Delta OCN\) (c – g – c) \( \Rightarrow OA = OC\) (cạnh tương ứng)

b) Ta có: \(\left\{ \begin{array}{l}OA = OC\\OB = OC\end{array} \right.\left( {cmt} \right) \Rightarrow OA = OB\)

\( \Rightarrow O\) cách đều hai đầu mút của đoạn thẳng AB

\( \Rightarrow O\) nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng)

Ứng với 1 cạnh của tam giác, ta có 1 đường cao

Vậy mỗi tam giác có 3 đường cao.