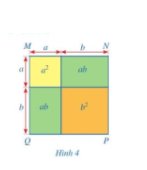
Diện tích của hình vuông MNPQ (hình 4) có thể được tính theo những cách nào?
Diện tích của hình vuông MNPQ (hình 4) có thể được tính theo những cách nào?

Xét hai biểu thức: \(P = 2\left( {x + y} \right)\) và \(Q = 2{\rm{x}} + 2y\)
Tính giá trị của mỗi biểu thức P và Q rồi so sánh hai giá trị đó trong mỗi trường hợp sau:
a) Tại x = 1; y = -1
b) Tại x = 2; y = -3
a) * Thay x = 1; y = -1 vào biểu thức P ta được:
\(P = 2.\left[ {1 + \left( { - 1} \right)} \right] = 0\)
Thay x = 1; y = -1 vào biểu thức Q ta được:
\(Q = 2.1 + 2.\left( { - 1} \right) = 0\)
\(\Rightarrow\) Tại x = 1; y = -1, P = Q.
b) * Thay x = 2; y = 3 vào biểu thức P ta được:
\(P = 2.\left( {2 + 3} \right) = 10\)
* Thay x = 2; y = 3 vào biểu thức Q ta được:
\(Q = 2.2 + 2.3 = 10\)
\(\Rightarrow\) Tại x = 2; y = 3, P = Q.
Trả lời bởi Hà Quang MinhChứng minh rằng: \(x\left( {x{y^2} + y} \right) - y\left( {{x^2}y + x} \right) = 0\).
Ta có: \(\begin{array}{l}x\left( {x{y^2} + y} \right) - y\left( {{x^2}y + x} \right)\\ = x.x{y^2} + xy - y.{x^2}y - {\rm{yx}}\\ = {x^2}{y^2} + xy - {x^2}{y^2} - xy = \left( {{x^2}{y^2} - {x^2}{y^2}} \right) + \left( {xy - xy} \right) = 0\end{array}\)
Vậy \(x\left( {x{y^2} + y} \right) - y\left( {{x^2}y + x} \right) = 0\) (đpcm)
Trả lời bởi Hà Quang MinhVới a, b là hai số thực bất kì, thực hiện phép tính:
a) \(\left( {a + b} \right)\left( {a + b} \right)\)
b) \(\left( {a - b} \right)\left( {a - b} \right)\)
a)
Cách 1: Diện tích hình vuông MNPQ là: \({a^2} + ab + ab + {b^2} = {a^2} + 2{\rm{a}}b + {b^2}\)
Cách 2: Độ dài cạnh của hình vuông MNPQ là: \(a + b\)
Diện tích của hình vuông MNPQ là: \(\left( {a + b} \right).\left( {a + b} \right) = {\left( {a + b} \right)^2}\)
b) \(\left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ab + b.b = {a^2} + 2{\rm{a}}b + {b^2}\)
c) \(\left( {a - b} \right)\left( {a - b} \right) = a.a - a.b - a.b - b.\left( { - b} \right) = {a^2} - 2{\rm{a}}b + {b^2}\)
Trả lời bởi Hà Quang MinhTính:
\(a){\left( {x + \dfrac{1}{2}} \right)^2}\)
\(b){\left( {2{\rm{x}} + y} \right)^2}\)
\(c){\left( {3 - x} \right)^2}\)
\(d){\left( {x - 4y} \right)^2}\)
\(a){\left( {x + \dfrac{1}{2}} \right)^2} = {x^2} + 2.x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = {x^2} + x + \dfrac{1}{4}\)
\(b){\left( {2{\rm{x}} + y} \right)^2} = {\left( {2{\rm{x}}} \right)^2} + 2.2{\rm{x}}.y + {y^2} = 4{{\rm{x}}^2} + 4{\rm{x}}y + {y^2}\)
\(c){\left( {3 - x} \right)^2} = {3^2} - 2.3.x + {x^2} = 9 - 6{\rm{x}} + {x^2}\)
\(d){\left( {x - 4y} \right)^2} = {x^2} - 2.x.4y + {\left( {4y} \right)^2} = {x^2} - 8{\rm{x}}y + 16{y^2}\)
Trả lời bởi Hà Quang MinhVới mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) \({y^2} + y + \dfrac{1}{4}\)
b) \({y^2} + 49 - 14y\)
a) \({y^2} + y + \dfrac{1}{4} = {y^2} - 2.y.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = {\left( {y - \dfrac{1}{2}} \right)^2}\)
b) \({y^2} + 49 - 14y = {y^2} - 14y + 49 = {y^2} - 2.y.7 + {7^2} = {\left( {y - 7} \right)^2}\)
Trả lời bởi Hà Quang MinhTính nhanh: \({49^2}\)
Ta có: \({49^2} = {\left( {50 - 1} \right)^2} = {50^2} - 2.50.1 + {1^2} = 2500 - 100 - 1 = 2401\)
Vậy: \({49^2} = 2401\)
Trả lời bởi Hà Quang MinhVới a, b là hai số thực bất kì, thực hiện phép tính: \(\left( {a - b} \right)\left( {a + b} \right)\)
\(\left( {a - b} \right)\left( {a + b} \right) = a.a + a.b - ba - b.b = {a^2} - {b^2}\)
Trả lời bởi Hà Quang MinhViết mỗi biểu thức sau dưới dạng tích:
a) \(9{{\rm{x}}^2} - 16\)
b) \(25 - 16{y^2}\)
a) \(9{{\rm{x}}^2} - 16 = {\left( {3{\rm{x}}} \right)^2} - {4^2} = \left( {3{\rm{x}} - 4} \right)\left( {3{\rm{x}} + 4} \right)\)
b) \(25 - 16{y^2} = {5^2} - {\left( {4y} \right)^2} = \left( {5 - 4y} \right)\left( {5 + 4y} \right)\)
Trả lời bởi Hà Quang MinhTính:
\(a)\left( {a - 3b} \right)\left( {a + 3b} \right)\)
\(b)\left( {2{\rm{x}} + 5} \right)\left( {2{\rm{x}} - 5} \right)\)
\(c)\left( {4y - 1} \right)\left( {4y + 1} \right)\)
\(a)\left( {a - 3b} \right)\left( {a + 3b} \right) = {a^2} - {\left( {3b} \right)^2} = {a^2} - 9{b^2}\)
\(b)\left( {2{\rm{x}} + 5} \right)\left( {2{\rm{x}} - 5} \right) = {\left( {2{\rm{x}}} \right)^2} - {5^2} = 4{{\rm{x}}^2} - 25\)
\(c)\left( {4y - 1} \right)\left( {4y + 1} \right) = {\left( {4y} \right)^2} - {1^2} = 16{y^2} - 1\)
Trả lời bởi Hà Quang Minh
Cách 1: Diện tích hình vuông MNPQ là: \({a^2} + ab + ab + {b^2} = {a^2} + 2{\rm{a}}b + {b^2}\)
Cách 2: Độ dài cạnh của hình vuông MNPQ là: \(a + b\)
Diện tích của hình vuông MNPQ là: \(\left( {a + b} \right).\left( {a + b} \right) = {\left( {a + b} \right)^2}\)
Trả lời bởi Hà Quang Minh