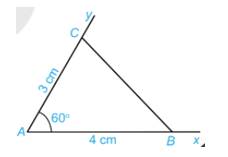
Vẽ \(\widehat {xAy}\) = 60°. Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27)
Vẽ thêm tam giác A’B’C’ với \(\widehat {B'A'C'}\)= 60°, A’B’ = 4 cm và A'C'= 3 cm (H.4.28).
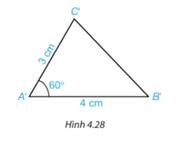
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và ABC.
- Hai tam giác ABC và ABC có bằng nhau không?
- Độ dài các cạnh AB và AB của hai tam giác em vừa vẽ có bằng các cạnh AB và AB của hai tam giác các bạn khác về không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
- Độ dài các cạnh tương ứng của 2 tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và A'B'C' có bằng nhau.
- Độ dài các cạnh AB' và AC' của hai tam giác em vừa vẽ có bằng các cạnh AB' và AC' của hai tam giác các bạn khác vẽ.
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ.
Trả lời bởi Hà Quang MinhTrong Hình 4.29, hai tam giác nào bằng nhau?
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
Trả lời bởi Hà Quang MinhHai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?
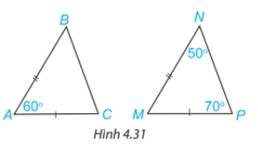
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
Trả lời bởi Hà Quang MinhCho Hình 4.32, biết \(\widehat {OAB} = \widehat {ODC},OA = OD\) và \(AB = CD\).
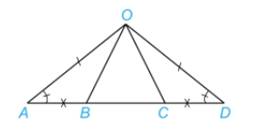
Chứng minh rằng:
a) \(AC = DB\);
b) \(\Delta OAC = \Delta ODB\).
a) Ta có:
\(\begin{array}{l}AB = CD\\ \Rightarrow AB + BC = CD + BC\\ \Rightarrow AC = BD\end{array}\)
b) Xét tam giác OAC và ODB có:
\(AC=BD\) (cmt)
\(\widehat A = \widehat D\) (gt)
\(OA=OD\) (gt)
\(\Rightarrow \Delta OAC = \Delta ODB\)(c.g.c)
Trả lời bởi Hà Quang MinhVẽ đoạn thẳng \(BC = 3\;{\rm{cm}}\). Vẽ hai tia Bx và Cy sao cho \(\widehat {xBC} = {80^\circ },\widehat {yCB} = {40^\circ }\) như Hình 4.33.
Lấy giao điểm \(A\) của hai tia Bx và Cy, ta được tam giác ABC (H.4.33).
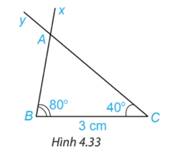
Vẽ thêm tam giác \({A^\prime }{B^\prime }{C^\prime }\) sao cho \({B^\prime }{C^\prime } = 3\;{\rm{cm}}\), \(\widehat {{A^\prime }{B^\prime }{C^\prime }} = {80^\circ },\widehat {{A^\prime }{C^\prime }{B^\prime }} = {40^\circ }.({\rm{H}}.4.34)\).
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\).
Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không?
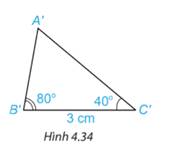
A’B’=2,2 cm
A’C’=3,4 cm
Hai tam giác \(ABC\) và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
Trả lời bởi Hà Quang MinhHai tam giác nào trong Hình 4.35 bằng nhau?
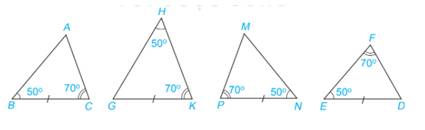
Cặp tam giác bằng nhau là:
\(\Delta ABC = \Delta MNP\) vì
\(\begin{array}{l}\widehat B = \widehat N( = 50^\circ )\\BC = NP\\\widehat C = \widehat P( = 70^\circ )\end{array}\)
Vậy \(\Delta ABC = \Delta MNP\) (g-c-g)
Trả lời bởi Hà Quang MinhChứng minh hai tam giác ABD và CBD trong hình 4.37 bằng nhau.
Xét hai tam giác ABD và CBD có:
\(\widehat {ABD} = \widehat {CBD}\)
BD chung
\(\widehat {ADB} = \widehat {CDB}\)
\(\Rightarrow \Delta ABD = \Delta CBD\)(g.c.g)
Trả lời bởi Hà Quang MinhBạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?
Do hai tam giác trên có hai cặp góc bằng nhau nên cặp góc còn lại bằng nhau.
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\widehat A = \widehat {A'}\) (gt)
AC = A'C' (gt)
\(\widehat C = \widehat {C'}\) (cmt)
\(\Rightarrow \Delta ABC = \Delta A'B'C'\) (g.c.g)
Vậy hai tam giác đã cho bằng nhau theo trường hợp góc – cạnh – góc.
Trả lời bởi Hà Quang Minh
Dùng thước thẳng có vạch chia đo độ dài cạnh BC ta được: BC=3,6cm.
Trả lời bởi Hà Quang Minh