Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Các câu hỏi tương tự
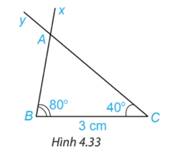
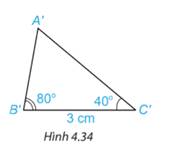
Vẽ thêm tam giác {A^prime }{B^prime }{C^prime } sao cho {B^prime }{C^prime } 3;{rm{cm}}, widehat {{A^prime }{B^prime }{C^prime }} {80^circ },widehat {{A^prime }{C^prime }{B^prime }} {40^circ }.({rm{H}}.4.34).Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác A B C và {A^prime }{B^prime }{C^prime }.Hai tam giác A B C và {A^prime }{B^prime }{C^prime } có bằng nhau không?
Đọc tiếp
Vẽ thêm tam giác \({A^\prime }{B^\prime }{C^\prime }\) sao cho \({B^\prime }{C^\prime } = 3\;{\rm{cm}}\), \(\widehat {{A^\prime }{B^\prime }{C^\prime }} = {80^\circ },\widehat {{A^\prime }{C^\prime }{B^\prime }} = {40^\circ }.({\rm{H}}.4.34)\).
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\).
Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không?
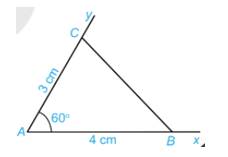
Vẽ \(\widehat {xAy}\) = 60°. Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27)
Vẽ thêm tam giác A’B’C’ với widehat {BAC} 60°, A’B’ 4 cm và AC 3 cm (H.4.28).Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và ABC.- Hai tam giác ABC và ABC có bằng nhau không?- Độ dài các cạnh AB và AB của hai tam giác em vừa vẽ có bằng các cạnh AB và AB của hai tam giác các bạn khác về không?- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
Đọc tiếp
Vẽ thêm tam giác A’B’C’ với \(\widehat {B'A'C'}\)= 60°, A’B’ = 4 cm và A'C'= 3 cm (H.4.28).
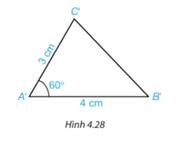
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và ABC.
- Hai tam giác ABC và ABC có bằng nhau không?
- Độ dài các cạnh AB và AB của hai tam giác em vừa vẽ có bằng các cạnh AB và AB của hai tam giác các bạn khác về không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:

a) \(\Delta \)ABE =\(\Delta \)DCE;
b) EG = EH.
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.
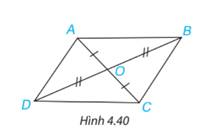
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng \(\Delta \)DAB = \(\Delta \)BCD.
Cho Hình 4.32, biết \(\widehat {OAB} = \widehat {ODC},OA = OD\) và \(AB = CD\).
Chứng minh rằng:
a) \(AC = DB\);
b) \(\Delta OAC = \Delta ODB\).
Chứng minh hai tam giác ABD và CBD trong hình 4.37 bằng nhau.

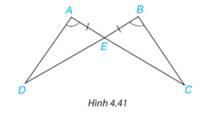
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.