Hãy giải thích tại sao sin35° = cos55°, tan35° = cot55°.
Bài 11. Tỉ số lượng giác của góc nhọn
H24
Hướng dẫn giải
Thảo luận (1)
H24
Sử dụng MTCT tính các tỉ số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:
a) sin40°54’;
b) cos52°15’;
c) tan69°36’;
d) cot25°18’.
Hướng dẫn giải
Thảo luận (1)
a) \(\sin {40^0}54'\)
Ta có: \(\sin {40^0}54' = 0,6547408137 \approx 0,655\)
b) \(\cos {52^0}15'\)
Ta có: \(\cos {52^0}15' = 0,61221728 \approx 0,612\)
c) \(\tan {69^0}36'\)
Ta có: \(\tan {69^0}36' = 2,688918967 \approx 2,689\)
d) \(\cot {25^0}18'\)
Ta có: \(\tan {25^0}18' = 0,4726978344\) nên \(\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}} = 2,115516356 \approx 2,116\)
Trả lời bởi datcoder
H24
Cho tam giác ABC vuông cân tại A và AB AC a (H.4.7a).a) Hãy tính BC và các tỉ số dfrac{AB}{BC},dfrac{AC}{BC}. Từ đó suy ra sin45°, cos45°.b) Hãy tính các tỉ số dfrac{AB}{AC} và dfrac{AC}{AB}. Từ đó suy ra tan45°, cot45°.
Đọc tiếp
Cho tam giác ABC vuông cân tại A và AB = AC = a (H.4.7a).
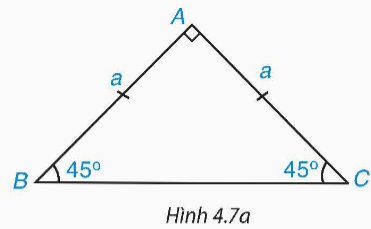
a) Hãy tính BC và các tỉ số \(\dfrac{AB}{BC},\dfrac{AC}{BC}\). Từ đó suy ra sin45°, cos45°.
b) Hãy tính các tỉ số \(\dfrac{AB}{AC}\) và \(\dfrac{AC}{AB}\). Từ đó suy ra tan45°, cot45°.
Hướng dẫn giải
Thảo luận (1)
Tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {a^2} + {a^2} = 2{a^2}\) suy ra \(BC = a\sqrt 2 \)
a) Tỉ số \(\frac{{AB}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) và \(\frac{{AC}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\).
Do đó \(\sin {45^0} = \sin \widehat B = \frac{{AC}}{{BC}} = \frac{{\sqrt 2 }}{2};\) \(\cos {45^0} = \cos \widehat B = \frac{{AB}}{{BC}} = \frac{{\sqrt 2 }}{2}.\)
b) Tỉ số \(\frac{{AB}}{{AC}} = \frac{a}{a} = 1;\) \(\frac{{AC}}{{AB}} = \frac{a}{a} = 1\)
Do đó \(\tan {45^0} = \tan \widehat B = \frac{{AC}}{{AB}} = 1;\) \(\cot {45^0} = \cot \widehat B = \frac{{AB}}{{AC}} = 1\)
Trả lời bởi datcoder
H24
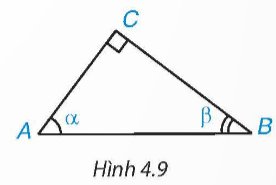
Cho tam giác ABC vuông tại C, có \(\widehat{A}\) = α, \(\widehat{B}\) = β (H.4.9). Hãy viết các tỉ số lượng giác của góc α, β theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
Hướng dẫn giải
Thảo luận (1)
Ta có:
\(\sin \alpha = \frac{{BC}}{{AB}};\) \(\cos \alpha = \frac{{AC}}{{AB}};\) \(\tan \alpha = \frac{{BC}}{{AC}};\) \(\cot \alpha = \frac{{AC}}{{BC}}\)
\(\sin \beta = \frac{{AC}}{{AB}};\) \(\cos \beta = \frac{{BC}}{{AB}};\) \(\tan \beta = \frac{{AC}}{{BC}};\) \(\cot \beta = \frac{{BC}}{{AC}}\)
Từ đó ta có
\(\sin \alpha = \cos \beta ;\) \(\cos \alpha = \sin \beta ;\) \(\tan \alpha = \cot \beta ;\) \(\cot \alpha = \tan \beta .\)
Trả lời bởi datcoder
H24
Xét tam giác đều ABC có cạnh bằng 2a.
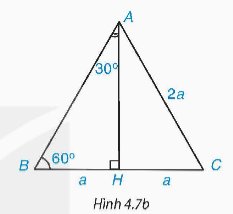
a) Tính đường cao AH của tam giác ABC (H.4.7b).
b) Tính sin30°, cos30°, sin60° và cos60°.
c) Tính tan30°, cot30°, tan60° và cot60°.
Hướng dẫn giải
Thảo luận (1)
a) Tam giác ABC đều có đường cao AH nên AH cũng là đường trung tuyến của tam giác. Do đó ta có H là trung điểm của BC nên \(BH = HC = \frac{{BC}}{2} = \frac{{2a}}{2} = a\)
Xét tam giác ABH vuông tại H, ta có: \(A{B^2} = A{H^2} + H{B^2}\) (Đjnh lý Pythagore)
Suy ra \({\left( {2a} \right)^2} = A{H^2} + {a^2}\) nên \(A{H^2} = 3a\) hay \(AH = a\sqrt 3 \)
b) Tam giác ABC đều nên \(\widehat A = \widehat B = \widehat C = {60^0}\)
Nên \(\cos {60^0} = \cos \widehat B = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\sin {60^0} = \sin \widehat B = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác của góc A, do đó \(\widehat {BAH} = \widehat {CAH} = \frac{{\widehat {BAC}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\)
\(\sin {30^0} = \sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\cos {30^0} = \cos \widehat {BAH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
c) \(\tan {30^0} = \tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
\(\cot {30^0} = \cot \widehat {BAH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\tan {60^0} = \tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\cot {60^0} = \tan \widehat {ABH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
Trả lời bởi datcoder
H24
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Hướng dẫn giải
Thảo luận (1)
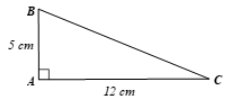
Xét tam giác ABC vuông tại A, ta có \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {5^2} + {12^2} = 169\) suy ra \(BC = 13\) (cm) .
Theo định nghĩa của tỉ số lượng giác ta có:
\(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{12}}{{13}};\\\cos \widehat B = \frac{{AB}}{{BC}} = \frac{5}{{13}};\\\tan \widehat B = \frac{{AC}}{{AB}} = \frac{{12}}{5};\\\cot \widehat B = \frac{{AB}}{{AC}} = \frac{5}{{12}}\)
Trả lời bởi datcoder
H24
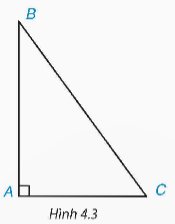
Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Hướng dẫn giải
Thảo luận (1)
Góc C có cạnh đối là AB và cạnh kề của góc C là AC.
Trả lời bởi datcoder
H24
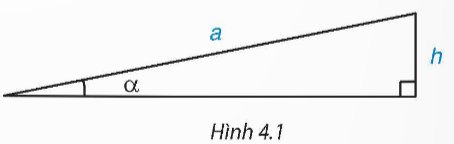
Ta có thể xác định “góc dốc” α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1). (Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn 6°).
Hướng dẫn giải
Thảo luận (1)
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Theo định nghĩa tỉ số lượng giác sin, ta có \(\sin\alpha=\dfrac{h}{a}\).
Vậy ta sẽ xác định được “góc dốc” α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h.
Trả lời bởi datcoder
H24
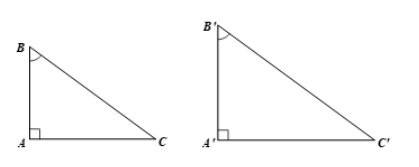
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat{B}=\widehat{B'}=\alpha\).Chứng minh rằng:
a) \(\Delta ABC\text{ᔕ}\Delta A'B'C'\);
b) \(\dfrac{AC}{BC}=\dfrac{A'C'}{B'C'};\dfrac{AB}{BC}=\dfrac{A'B'}{B'C'};\dfrac{AC}{AB}=\dfrac{A'C'}{A'B'};\dfrac{AB}{AC}=\dfrac{A'B'}{A'C'}\).
Hướng dẫn giải
Thảo luận (1)
a) Xét hai tam giác ABC và tam giác A’B’C’ ta có:
\(\begin{array}{l}\widehat A = \widehat {A'} = {90^0}\\\widehat B = \widehat {B'} = \alpha \end{array}\)
Nên \(\Delta ABC\backsim \Delta A'B'C'\left( g-g \right)\)
b) \(\Delta ABC\backsim \Delta A'B'C'\) suy ra \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) (tỉ lệ các cạnh tương ứng)
Do \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) nên ta có \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) (tính chất tỉ lệ thức)
Do \(\frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{A'C'}}{{B'C'}} = \frac{{AC}}{{BC}}\) (tính chất tỉ lệ thức)
Do \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\) và \(\frac{{AC}}{{AB}} = \frac{{A'B'}}{{A'C'}}\) (tính chất tỉ lệ thức)
Trả lời bởi datcoder
H24
Cho tam giác ABC vuông tại A có \(\widehat{C}\) = 45° và AB = c. Tính BC và AC theo c.
Hướng dẫn giải
Thảo luận (1)
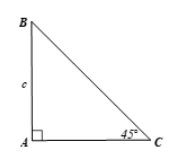
Ta có: \(\tan \widehat C = \frac{{AB}}{{AC}}\) suy ra \(\tan {45^0} = \frac{c}{{AC}}\) do đó \(1 = \frac{c}{{AC}}\) hay \(AC = c\)
\(\sin \widehat C = \frac{{AB}}{{BC}}\) suy ra \(\sin {45^0} = \frac{c}{{BC}}\) do đó \(\frac{{\sqrt 2 }}{2} = \frac{c}{{BC}}\) hay \(BC = \frac{{2c}}{{\sqrt 2 }} = \sqrt 2 c\)
Trả lời bởi datcoder
Vì \({35^0} + {55^0} = {90^0}\) nên \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)
Trả lời bởi datcoder