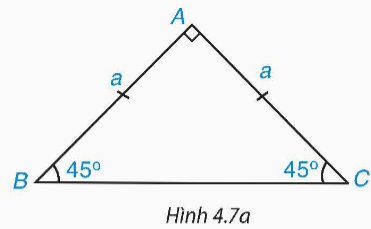
Tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {a^2} + {a^2} = 2{a^2}\) suy ra \(BC = a\sqrt 2 \)
a) Tỉ số \(\frac{{AB}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) và \(\frac{{AC}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\).
Do đó \(\sin {45^0} = \sin \widehat B = \frac{{AC}}{{BC}} = \frac{{\sqrt 2 }}{2};\) \(\cos {45^0} = \cos \widehat B = \frac{{AB}}{{BC}} = \frac{{\sqrt 2 }}{2}.\)
b) Tỉ số \(\frac{{AB}}{{AC}} = \frac{a}{a} = 1;\) \(\frac{{AC}}{{AB}} = \frac{a}{a} = 1\)
Do đó \(\tan {45^0} = \tan \widehat B = \frac{{AC}}{{AB}} = 1;\) \(\cot {45^0} = \cot \widehat B = \frac{{AB}}{{AC}} = 1\)