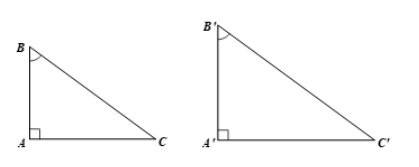
a) Xét hai tam giác ABC và tam giác A’B’C’ ta có:
\(\begin{array}{l}\widehat A = \widehat {A'} = {90^0}\\\widehat B = \widehat {B'} = \alpha \end{array}\)
Nên \(\Delta ABC\backsim \Delta A'B'C'\left( g-g \right)\)
b) \(\Delta ABC\backsim \Delta A'B'C'\) suy ra \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) (tỉ lệ các cạnh tương ứng)
Do \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) nên ta có \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) (tính chất tỉ lệ thức)
Do \(\frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{A'C'}}{{B'C'}} = \frac{{AC}}{{BC}}\) (tính chất tỉ lệ thức)
Do \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\) và \(\frac{{AC}}{{AB}} = \frac{{A'B'}}{{A'C'}}\) (tính chất tỉ lệ thức)

