Bài 1. Hai tam giác đồng dạng

KHÔNG

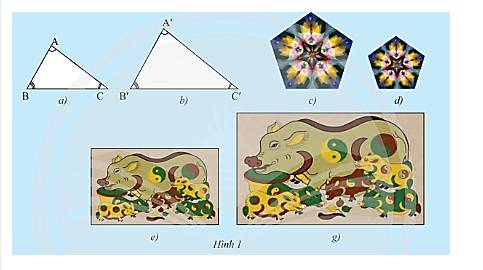
Hình dạng và kích thước của các hình này tỉ lệ với nhau

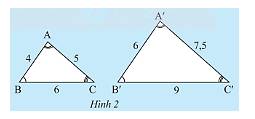
a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là:

\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)

b) Ta có:

\(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\).

Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\)

a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\)  nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng)

Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\).

b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \)

Vậy \(\widehat {AMN} = 65^\circ \).

a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.

Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.

b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).

Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).

Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).

Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)

Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)

\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)

\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)

Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)

Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)

\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)

\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)

Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)

Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).

Vậy tỉ số đồng dạng là \(\frac{1}{4}\).

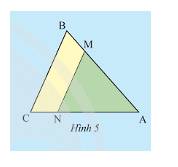
Vì \(MN//BC\) nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị)

Xét tam giác \(ABC\) có, \(MN//BC\) nên theo hệ quả của định lí Thales ta có:

\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).

Vậy trong các ô trống cần điền là:

\(\widehat A\) chung;

\(\widehat M = \widehat B\);

\(\widehat N = \widehat C\);

\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).

Tam giác \(\Delta AMN\) và\(\Delta ABC\) có các góc tương ứng bằng nhau và tỉ số các cạnh tương ứng bằng nhau nên \(\Delta AMN\) đồng dạng \(\Delta ABC\).

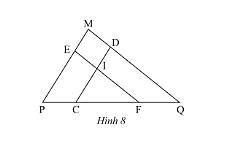
a) Xét tam giác \(MPQ\)có  \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)

Xét tam giác \(MPQ\)có  \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)

Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)

b) Xét tam giác \(EPF\)có  \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)

Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).

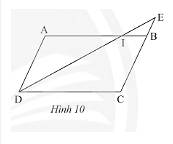
a) Do \(ABCD\) là hình bình hành nên \(BC//AD \Rightarrow EB//AD\)

Xét tam giác \(IDA\) có

\(EB//AD;EB\) cắt \(AI;ID\) tại \(B;E\).

Do đó, \(\Delta IEB\backsim\Delta IDA\) (định lí)

b) Ta có: \(\Delta IEB\backsim\Delta IDA \Rightarrow \frac{{IB}}{{IA}} = \frac{{BE}}{{DA}}\) (hai cặp cạnh tương ứng tỉ lệ).

Mà \(CB = AD;CB = 3BE \Rightarrow AD = 3BE;AI = 9\) nên ta có:

\(\frac{{IB}}{9} = \frac{{BE}}{{3BE}} = \frac{1}{3} \Rightarrow IB = \frac{{9.1}}{3} = 3\).

Vậy \(IB = 3cm.\)

Khẳng định đúng là a, khẳng định sai là b.

- Khẳng định a đúng vì

Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.

Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.

- Khẳng định b sai vì

Nếu\(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) thì tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).

Khi \(k \ne 1\) thì \(AB \ne A'B'AC \ne A'C'BC \ne B'C'\) nên hai tam giác không bằng nhau.