Question

Xét tính đơn điệu và tìm cực trị của hàm số:

a) y=x+\(\sqrt{9-x^2}\)

b) y=\(\dfrac{-x^2-x-2}{x+2}\)

Answer 1

a. ĐKXĐ: \(-3\le x\le3\)

\(y'=1-\dfrac{x}{\sqrt{9-x^2}}=\dfrac{\sqrt{9-x^2}-x}{\sqrt{9-x^2}}=0\Rightarrow x=\dfrac{3\sqrt{2}}{2}\)

Dấu của y':

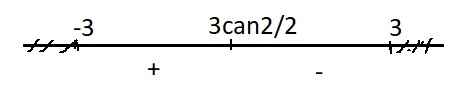
Hàm đồng biến trên \(\left(-3;\dfrac{3\sqrt{2}}{2}\right)\) và nghịch biến trên \(\left(\dfrac{3\sqrt{2}}{2};3\right)\)

b.

ĐKXĐ: \(x\ne2\)

\(y'=\dfrac{\left(-2x-1\right)\left(x+2\right)+x^2+x+2}{\left(x+2\right)^2}=\dfrac{-x^2-4x}{\left(x+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)

Dấu của y':

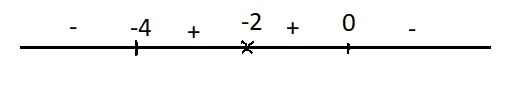
Hàm đồng biến trên các khoảng \(\left(-4;-2\right)\) và \(\left(-2;0\right)\)

Hàm nghịch biến trên các khoảng \(\left(-\infty;-4\right)\) và \(\left(0;+\infty\right)\)