Muốn câu hỏi mình xuất hiện trong chuyên mục? Gửi ngay câu hỏi tới: https://forms.gle/PBruN2d3LXicucxu6. Chúng mình sẽ duyệt những câu hỏi hay nhất!
Hãy tương tác với page Facebook nữa nha! Cuộc thi Trí tuệ VICE | Facebook
(2-4 điểm thưởng/1 ý làm)
| Toán.C27 _ 3.8.2021 | Rin Huỳnh (Hoc24) |



| Toán.C28 _ 3.8.2021 | Hir Dương (Hoc24) |
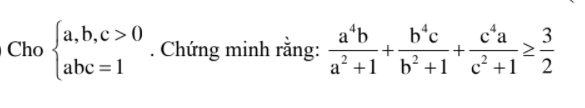
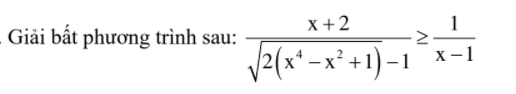
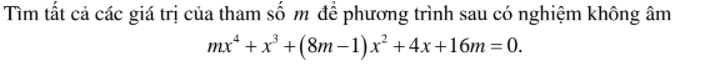

C27.1
Ta có: \(P=a^2+b^2+\dfrac{5}{a+b+1}=\left(a^2+1\right)+\left(b^2+1\right)+\dfrac{5}{a+b+ab+1+1}-2\)
\(\ge\dfrac{\left(a+1\right)^2}{2}+\dfrac{\left(b+1\right)^2}{2}+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}-2\)
\(\ge2\sqrt{\dfrac{\left(a+1\right)^2\left(b+1\right)^2}{4}}+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}-2\)
\(=\left(a+1\right)\left(b+1\right)+1+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}-3\)
\(=\dfrac{\left(a+1\right)\left(b+1\right)+1}{5}+\dfrac{5}{\left(a+1\right)\left(b+1\right)+1}+\dfrac{4\left(a+1\right)\left(b+1\right)+4}{5}-3\)
\(\ge2+\dfrac{4.2\sqrt{a}.2\sqrt{b}+4}{5}-3=2+\dfrac{4.4\sqrt{ab}+4}{5}-3=3\)
Dấu ''='' xảy ra khi và chỉ khi a=b=1
C28.1
Ta có VT=\(\dfrac{a^4b^2}{a^2b+b}+\dfrac{b^4c^2}{b^2c+c}+\dfrac{c^4a^2}{c^2a+a}\ge\dfrac{\left(a^2b+b^2c+c^2a\right)^2}{a^2b+b^2c+c^2a+a+b+c}\)
Vì \(\left(a^2b+b^2c+c^2a\right)^3\ge\left(a+b+c\right)^3\) ( Theo bđt holder)
\(\Leftrightarrow a^2b+b^2c+c^2a\ge a+b+c\)
\(\Rightarrow VT\ge\dfrac{\left(a^2b+b^2c+c^2a\right)^2}{2\left(a^2b+b^2c+c^2a\right)}=\dfrac{a^2b+b^2c+c^2a}{2}\ge\dfrac{3\sqrt[3]{\left(abc\right)^3}}{2}=\dfrac{3}{2}\)
Dấu ''='' xảy ra khi a=b=c
C28.1: Làm lại câu này là vì cách kia có holder nhìn hơi cấn:v
\(VT=\dfrac{a^4b^2}{a^2b+b}+\dfrac{b^4c^2}{b^2c+c}+\dfrac{c^4a^2}{c^2a+a}\ge\dfrac{\left(a^2b+b^2c+c^2a\right)^2}{a^2b+b^2c+c^2a+a+b+c}\)
Theo bđt Côsi ta có:
\(a^2b+c^2a+\dfrac{1}{bc^2}\ge3\sqrt[3]{\dfrac{a^3c^2b}{c^2b}}=3a\)
\(c^2a+b^2c+\dfrac{1}{ab^2}\ge3c\)
\(a^2b+b^2c+\dfrac{1}{a^2c}\ge3b\)
\(\Rightarrow2\left(a^2b+b^2c+c^2a\right)+\dfrac{1}{bc^2}+\dfrac{1}{ab^2}+\dfrac{1}{ca^2}\ge3\left(a+b+c\right)\)
\(\Leftrightarrow2\left(a^2b+b^2c+c^2\right)+\dfrac{a^2b+b^2c+c^2a}{a^2b^2c^2}\ge3\left(a+b+c\right)\)
\(\Leftrightarrow3\left(a^2b+b^2c+c^2a\right)\ge3\left(a+b+c\right)\Leftrightarrow a^2b+b^2c+c^2a\ge a+b+c\)
=> ..... (Làm như cách kia)
:3
ừ chúc bạn may mắn nhé thi tốt !!!!!
Toán C28, bài 5) tan5x=-38/41; tan(5x - pi/4)= -79/3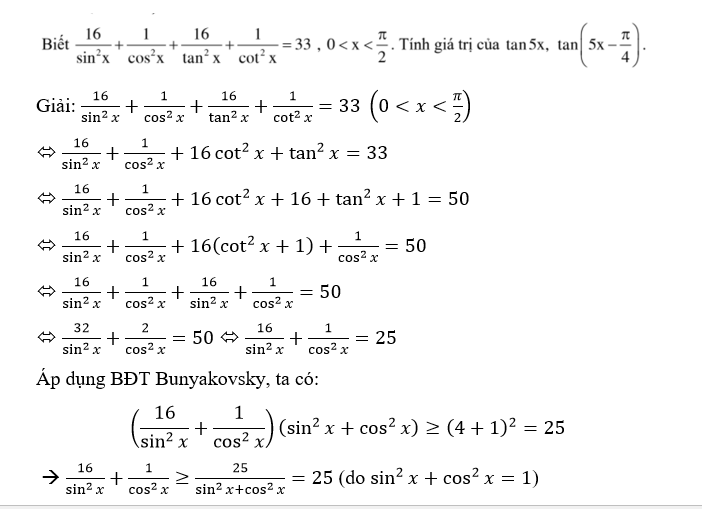
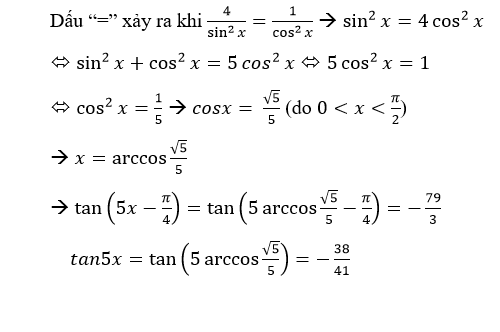










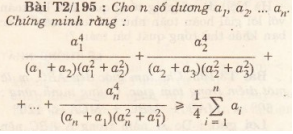
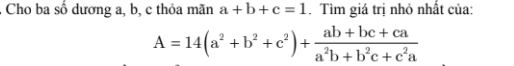
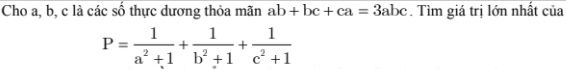
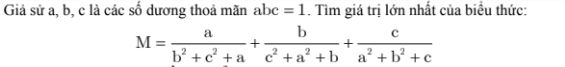




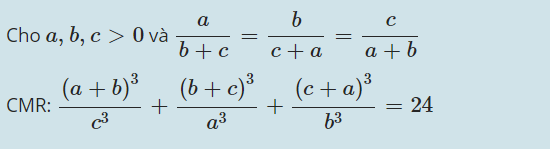


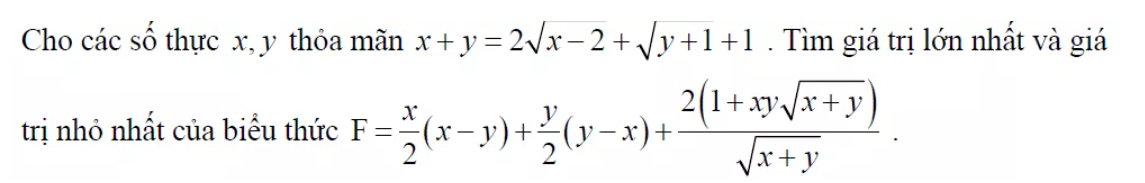
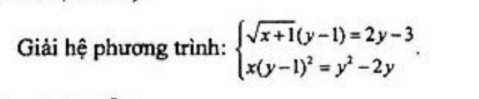
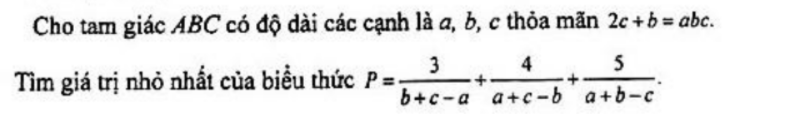
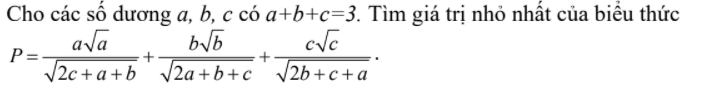




 4)
4)