Vẽ hình theo tỉ lệ:
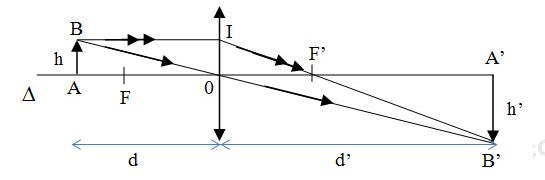
Ảnh A’B’ là ảnh thật, ngược chiều với vật.
- Xét ∆ABO và tam giác ∆A’B’O
Có: góc OAB = góc O'A B' ( đối đỉnh) ; góc A = góc A' = 90 độ
Nên ∆ABO ~ ∆A’B’O
Ta có các tỉ số đồng dạng:
\(\dfrac{AB}{A'B'}=\dfrac{AO}{A'O'}\Leftrightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\)
- Xét ∆OIF’ và ∆F’A’B’
Có:
\(\widehat{IF'O}=\widehat{B'F'A'};\widehat{O}=\widehat{A'}=90^o\)
Nên ∆OIF’ ~ ∆F’A’B’ .
Ta có tỉ số đồng dạng:

Thay số từ đề bài ta có:

Vậy ảnh cách thấu kính 48 cm và A’B’ cao 3 cm.
c)
Từ biểu thức ở phần b ta biến đổi như sau:

Đặt khoảng cách giữa ảnh và vật là:  ; ta được
; ta được

Vì vật tạo ra ảnh thật nên ta có điều kiện là d > 0 và phương trình (*) có nghiệm. Tức là:

Vậy khoảng cách giữa vật và ảnh thật luôn lớn hơn hoặc bằng 4f.
Khoảng cách này ngắn nhất là 4f.
Khi đó giải phương trình (*) ta được d = 2f.

