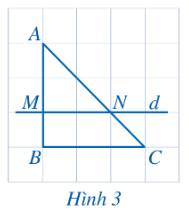
a) \(\frac{{AM}}{{MB}} = \frac{1}{2}\)
\(\frac{{AN}}{{AC}} = \frac{{1,5}}{3} = \frac{1}{2}\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
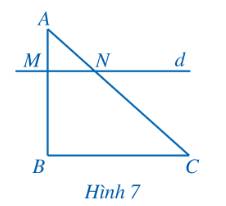
b) Qua B kẻ đường thẳng song song với đường thẳng d, cắt AC tại C’.
Xét ∆ABC’ với MN // BC’, ta có:
\( \frac{AM}{MB}=\frac{AN}{NC′}\) (định lí Thalès).
Mà theo câu a, \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) nên ta có \(\frac{{AN}}{{NC}} = \frac{AN}{NC′}\)
Suy ra NC = NC’ hay C và C’ là hai điểm trùng nhau.
Do đó C nằm trên đường thẳng đi qua B và song song với đường thẳng d.
Vậy đường thẳng d (đi qua M, N) song song với BC.