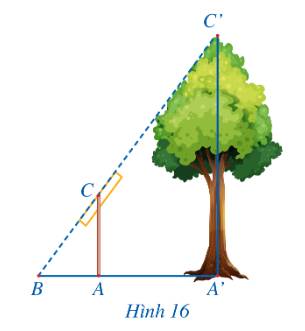
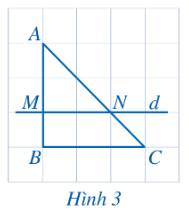
Xét tam giác ABC có
\(\begin{array}{l}\frac{{CM}}{{CA}} = \frac{1}{4}\\\frac{{CN}}{{CB}} = \frac{{1,25}}{5} = \frac{1}{4}\\ \Rightarrow \frac{{CM}}{{CA}} = \frac{{CN}}{{CB}}\end{array}\)
\( \Rightarrow MN\parallel AB\) (Định lý Thales đảo)
Mà \(AB \bot AC\) nên \(MN \bot AC\) hay tam giác MNC vuông tại M
Xét tam giác MNC vuông tại M có: \(MC = 1,\,\,NC = 1,25\).
Theo định lý Pytago ta có:
\(\begin{array}{l}M{N^2} + M{C^2} = N{C^2}\\\,\,\,\,\,\,\,M{N^2} + {1^2} = 1,{25^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 1,{25^2} - {1^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 0,5625\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,MN = 0,75\end{array}\)
Vậy MN = 0,75.