Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\) là trung điểm của \(SC\).
a) Tìm giao điểm \(I\) của đường thẳng \(AM\) và mặt phẳng \(\left( {SBD} \right)\). Chứng minh \(IA = 2IM\).
b) Tìm giao điểm \(E\) của đường thẳng \(S{\rm{D}}\) và mặt phẳng \(\left( {ABM} \right)\).
c) Gọi \(N\) là một điểm tuỳ ý trên cạnh \(AB\). Tìm giao điểm của đường thẳng \(MN\) và mặt phẳng \(\left( {SBD} \right)\).
Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\).
a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\).
b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
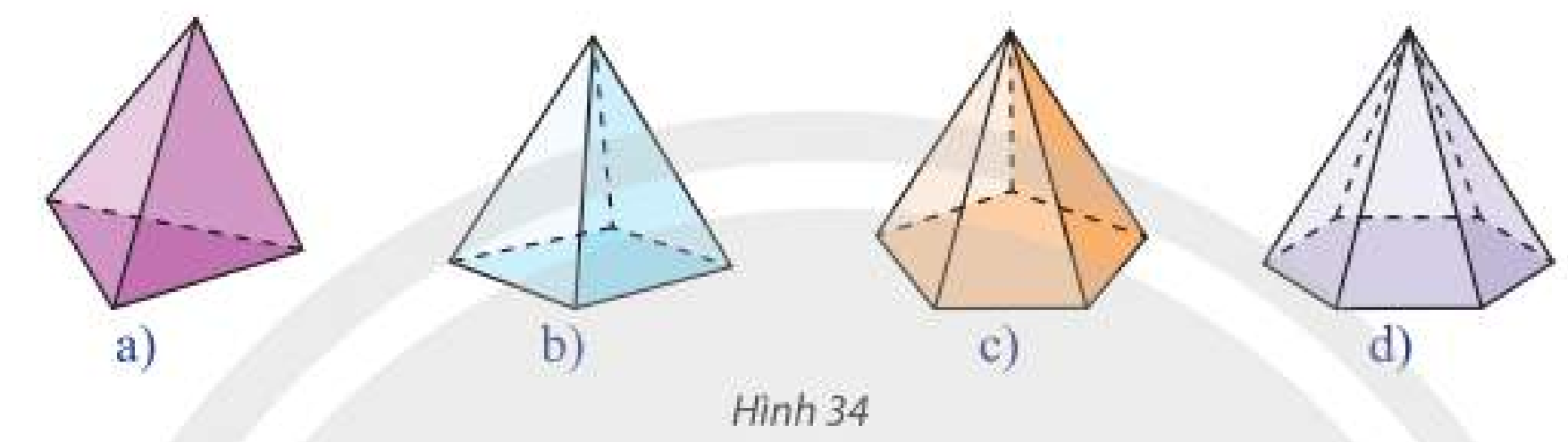
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?
a) Vẽ hình biểu diễn của một hình hộp chữ nhật.
b) Quan sát Hình 4a và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng \(\left( P \right)\).
c) Quan sát Hình 4b và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng \(\left( Q \right)\).
Trong mặt phẳng \(\left( P \right)\), cho tam giác \(ABC\) có \(M,N\) lần lượt là trung điểm của các đoạn thẳng \(AB,AC\) (Hình 17). Tính tỉ số \(\frac{{MN}}{{BC}}\).
Quan sát Hình 10 và cho biết người thợ mộc kiểm tra mặt bàn có phẳng hay không bằng một cây thước thẳng như thế nào.
Cho hình chóp \(S.ABCD\). Trên các cạnh bên của hình chóp lấy lần lượt các điểm \(A',B',C',D'\). Cho biết \(AC\) cắt \(B{\rm{D}}\) tại \(O\), \(A'C'\) cắt \(B'{\rm{D'}}\) tại \(O'\), \(AB\) cắt \(DC\) tại \(E\) và \(A'B'\) cắt \(D'C'\) tại \(E'\) (Hình 39). Chứng minh rằng:
a) \(S,O',O\) thẳng hàng;
b) \(S,E',E\) thẳng hàng.
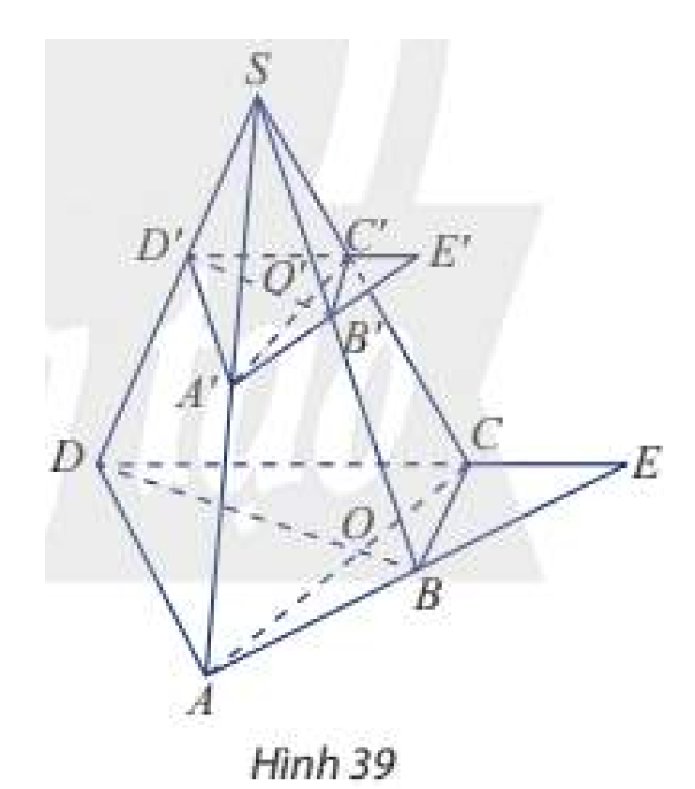
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD\); \(M,N\) lần lượt là trung điểm của \(SB,SD\); \(P\) thuộc đoạn \(SC\) và không là trung điểm của \(SC\).
a) Tìm giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \(\left( {MNP} \right)\).
b) Tìm giao điểm \(Q\) của đường thẳng \(SA\) và mặt phẳng \(\left( {MNP} \right)\).
c) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB\), \(QP\) và \(AC\), \(QN\) và \(A{\rm{D}}\). Chứng minh \(I,J,K\) thẳng hàng.
Mặt bàn, mặt bảng cho ta hình ảnh một phần của mặt phẳng. Hãy chỉ thêm các ví dụ khác về hình ảnh một phần của mặt phẳng.
