a) Vẽ hình biểu diễn của một hình hộp chữ nhật.
b) Quan sát Hình 4a và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng \(\left( P \right)\).
c) Quan sát Hình 4b và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng \(\left( Q \right)\).
Quan sát Hình 10 và cho biết người thợ mộc kiểm tra mặt bàn có phẳng hay không bằng một cây thước thẳng như thế nào.
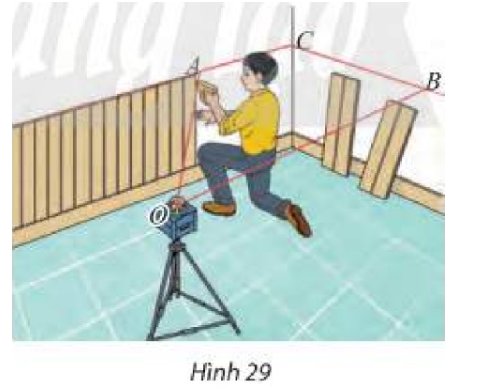
Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường trong Hình 29.
Quan sát Hình 13 và cho biết bốn đỉnh \(A,B,C,D\) của cái bánh giò có cùng nằm trên một mặt phẳng hay không.
Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\).
a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\).
b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Cho mặt phẳng \(\left( Q \right)\) đi qua bốn đỉnh của tứ giác \(ABCD\). Các điểm nằm trên các đường chéo của tứ giác \(ABCD\) có thuộc mặt phẳng \(\left( Q \right)\) không? Giải thích.
Hai đường thẳng phân biệt \(a\) và \(b\) cắt nhau tại điểm \(O\). Trên \(a,b\) lấy lần lượt hai điểm \(M,N\) khác \(O\). Gọi \(\left( P \right)\) là mặt phẳng đi qua ba điểm \(M,N,O\) (Hình 25). Mặt phẳng \(\left( P \right)\) có chứa cả hai đường thẳng \(a\) và \(b\) không? Giải thích.
Trong mặt phẳng \(\left( P \right)\), cho tam giác \(ABC\) có \(M,N\) lần lượt là trung điểm của các đoạn thẳng \(AB,AC\) (Hình 17). Tính tỉ số \(\frac{{MN}}{{BC}}\).
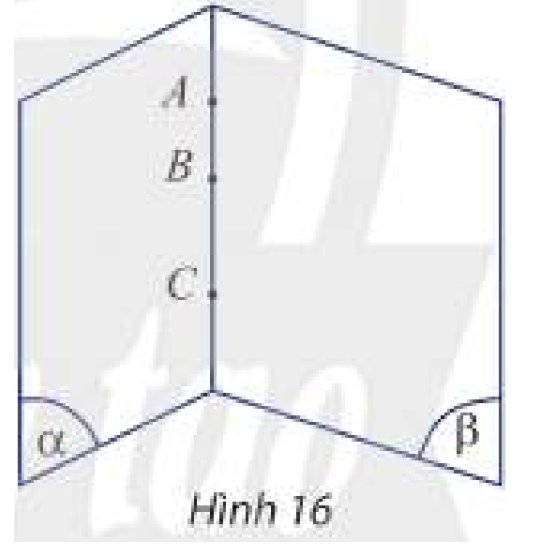
Cho \(A,B,C\) là ba điểm chung của hai mặt phẳng phân biệt \(\left( \alpha \right)\) và \(\left( \beta \right)\) (Hình 16). Chứng minh \(A,B,C\) thẳng hàng.
