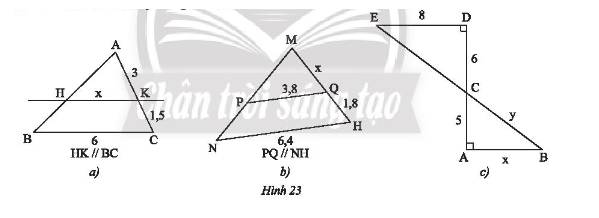
a) Ta có: \(AC = AK + KC = 3 + 1,5 = 4,5\)
Xét tam giác \(ABC\) có \(HK//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{HK}}{{BC}} = \frac{{AK}}{{AC}} \Rightarrow \frac{x}{6} = \frac{3}{{4,5}}\). Do đó, \(x = \frac{{3.6}}{{4,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MH = MQ + QH = x + 1,8\)
Xét tam giác \(MNH\) có \(PQ//NH\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{PQ}}{{NH}} = \frac{{MQ}}{{MH}} \Rightarrow \frac{{3,8}}{{6,4}} = \frac{x}{{x + 1,8}}\). Do đó, \(6,4x = 3,8.\left( {x + 1,8} \right)\)
\( \Leftrightarrow 6,4x = 3,8x + 6,84\)
\( \Leftrightarrow 6,4x - 3,8x = 6,84\)
\( \Leftrightarrow 2,6x = 6,84\)
\( \Leftrightarrow x = 6,84:2,6\)
\( \Leftrightarrow x = \frac{{171}}{{65}}\).
Vậy \(x = \frac{{171}}{{65}}\).
c) Vì \(\left\{ \begin{array}{l}DE \bot AD\\AB \bot AD\end{array} \right. \Rightarrow DE//AB\) (quan hệ từ vuông góc đến song song).
Xét \(\Delta CDE\) vuông tại \(D\) ta có:
\(E{D^2} + D{C^2} = E{C^2}\) (Định lí Py- ta – go)
\( \Leftrightarrow {8^2} + {6^2} = E{C^2}\)
\( \Leftrightarrow E{C^2} = 100\)
\( \Leftrightarrow EC = 10\)
Xét tam giác \(ABC\) có \(DE//AB\) nên theo hệ quả của định lí Thales ta có:
\(\left\{ \begin{array}{l}\frac{{AC}}{{DC}} = \frac{{AB}}{{ED}} \Rightarrow \frac{5}{6} = \frac{x}{8}\\\frac{{AC}}{{DC}} = \frac{{BC}}{{EC}} \Rightarrow \frac{5}{6} = \frac{y}{{10}}\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = \frac{{5.8}}{6} = \frac{{20}}{3}\\y = \frac{{5.10}}{6} = \frac{{25}}{3}\end{array} \right.\).
Vậy \(x = \frac{{20}}{3};y = \frac{{25}}{3}\).