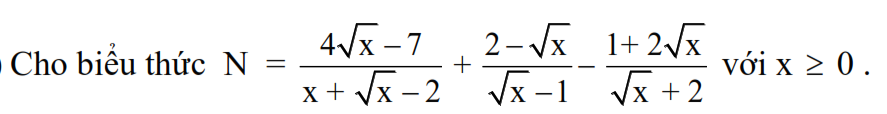\(n^2+2002=k^2\Rightarrow k^2-n^2=2002\)
\(\Rightarrow\left(k-n\right)\left(k+n\right)=2002\)
Do \(\left(k-n\right)+\left(k+n\right)=2k\) chẵn nên \(\left(k-n\right)\) và \(\left(k+n\right)\) cùng chẵn
Bạn chỉ cần xét các cặp ước chẵn của 2002
Ta thấy n2 chia cho 4 dư 0 hoặc 1 nên n2 + 2002 chia cho 4 dư 2 hoặc 3.
Do đó n2 + 2002 không thể là số chính phương.