\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1+2\sqrt{x}}\)
\(=\dfrac{x-1}{x-1+2\sqrt{x}}\)
Để \(P>0\)
\(\Rightarrow\dfrac{x-1}{x-1+2\sqrt{x}}>0\)
\(TH_1:x-1>0\Leftrightarrow x>1\)
\(TH_2:x-1+2\sqrt{x}>0\Leftrightarrow\left(\sqrt{x}+1\right)^2< 2\)
\(\Leftrightarrow-\sqrt{2}-1< \sqrt{x}< \sqrt{2}-1\)
\(\Leftrightarrow0< x< 3-2\sqrt{2}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}\left(x-1\right)}{x+2\sqrt{x}-1}\)
\(=\dfrac{\left(x-1\right)\left(\sqrt{x}+1\right)}{x+2\sqrt{x}-1}\)
Để P>0 thì (x-1)/(x+2căn x-1)>0
TH1: x-1>0 và x+2căn x-1>0
=>x>1
TH2: x-1<0 và x+2căn x-1<0
=>0<x<1 và (căn x+1)^2<2
=>0<x<1và \(-\sqrt{2}< \sqrt{x}+1< \sqrt{2}\)
=>\(\left\{{}\begin{matrix}0< x< 1\\-\sqrt{2}-1< \sqrt{x}< \sqrt{2}-1\end{matrix}\right.\Leftrightarrow0< x< 3-2\sqrt{2}\)
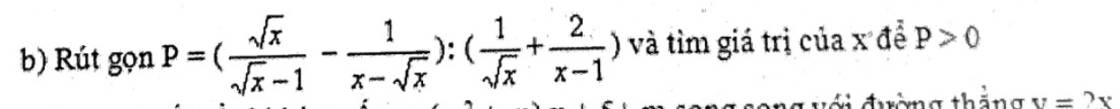 Tìm giúp em giá trị của x ạ. E xin cảm ơn
Tìm giúp em giá trị của x ạ. E xin cảm ơn






