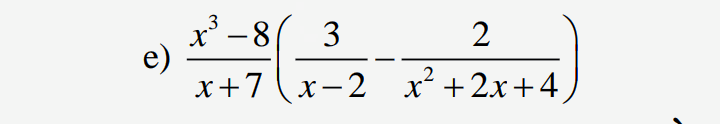\(\dfrac{x^3-8}{x+7}\left(\dfrac{3}{x-2}-\dfrac{2}{x^2+2x+4}\right)\\ =\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}\left(\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\right)\\ =\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}\left(\dfrac{3x^2+6x+12}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{2x-4}{\left(x-2\right)\left(x^2+2x+4\right)}\right)\)
\(=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}.\dfrac{3x^2+6x+12-2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3x^2+4x+16}{x+7}\)
\(=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}\cdot\dfrac{3x^2+6x+12-2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3x^2+4x+16}{x+7}\)