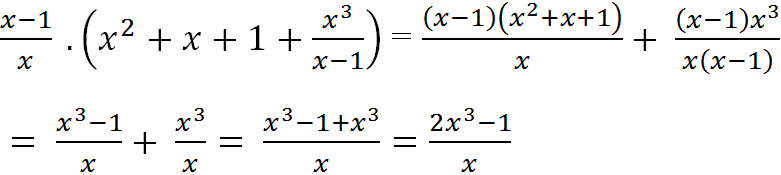Cách 1 \(\dfrac{x-1}{x}.\left(x^2+x+1+\dfrac{x^3}{x-1}\right)\\ =\dfrac{x-1}{x}.\left(\dfrac{\left(x-1\right)(x^2+x+1)+x^3}{x-1}\right)\\ =\dfrac{x-1}{x}.\dfrac{2x^3-1}{x-1}=\dfrac{2x^3-1}{x}\)
Cách 2 \(\dfrac{x-1}{x}.\left(x^2+x+1+\dfrac{x^3}{x-1}\right)\\ =\dfrac{x-1}{x}.\left(x^2+x+1\right)+\dfrac{x-1}{x}.\dfrac{x^3}{x-1}\\ =\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x}+x^2\\ =\dfrac{x^3-1}{x}+x^2=\dfrac{2x^3-1}{x}\)