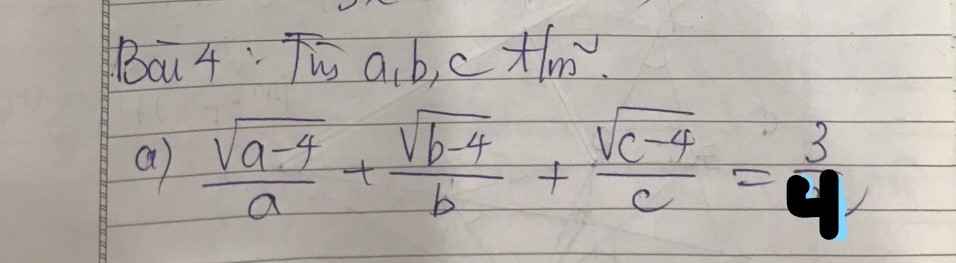\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(< =>\left(\dfrac{1}{a}+\dfrac{1}{b}\right).\left(a+b\right)\ge4\)
\(< =>1+\dfrac{b}{a}+\dfrac{a}{b}+1\ge4\)
\(< =>2+\dfrac{a}{b}+\dfrac{b}{a}\ge4\)(luôn đúng với mọi a,b là số thực dương)
Thật vậy có \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{a}{b}.\dfrac{b}{a}}=2\)(BĐT Cosi)
\(=>2+\dfrac{a}{b}+\dfrac{b}{a}\ge2+2=4\left(đpcm\right)\)
dấu"=" xảy ra<=>a=b