Một thấu kinh hội tụ có tiêu cự là \(f\). Gọi d và d' lần lượt là khoảng cách từ một vật thật AB từ ảnh A'B' của nó tới quang tâm O của thấu kính (h.54). Công thức thấu kính là : \(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\)
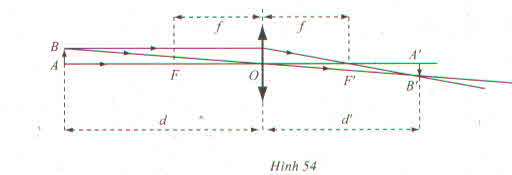
a) Tìm biểu thức xác định hàm số \(d'=\varphi\left(d\right)\)
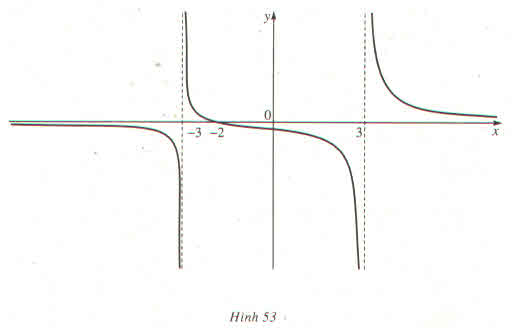
b) Tìm \(\lim\limits_{d\rightarrow f^+}\varphi\left(d\right);\lim\limits_{d\rightarrow f^-}\varphi\left(d\right)\) và \(\lim\limits_{d\rightarrow+\infty}\varphi\left(d\right)\)
Giải thích ý nghĩa của các kết quả tìm được ?
a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).