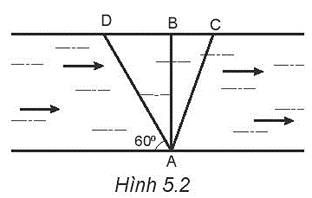
Một ca nô đi ngang qua sông, xuất phát từ điểm A, mũi hướng vào một điểm B trên bờ sông bên kia. AB vuông góc với bờ sông. Nhưng do dòng nước chảy nên sau một thời gian t=100s, ca nô đến một vị trí C ở bờ bên kia, cách B một đoạn BC =200 m. Nếu người lái giữ cho mũi ca nô luôn hướng theo phương chếch với bờ sông một góc 60 và mở máy như trước thì ca nô sẽ sang đến đúng điểm B. Hãy tìm: a. Vận tốc của dòng nước so với bờ sông. b. Vận tốc của ca nô so với dòng nước. c. Chiều rộng d của dòng sông. d. Thời gian để ca nô qua sông trong trường hợp ca nô cập bến B
Cho (1) là ca nô, (2) là nước, (3) là bờ sông.
(a) Trong 100s, nước chảy đưa ca nô chếch từ vị trí B đến C, nên vận tốc của dòng nước so với bờ là: \(v_{23}=\dfrac{BC}{t}=\dfrac{200}{100}=2\left(m/s\right)\)
(b) Dựa vào hình vẽ, dễ thấy: \(\hat{ADB}=\alpha=60^o\).
Khi đi theo hướng \(AD:v_{12}=v_{12}';v_{23}=v_{23}'=2\left(m/s\right)\)
\(v_{23}'\) là vận tốc của dòng nước so với bờ sông, tức vecto này hướng theo hướng vector \(\overrightarrow{DB}\), \(v_{12}'\) là vận tốc của ca nô so với dòng nước, tức vecto này theo hướng vector \(\overrightarrow{AD}\).
Dựa vào hình vẽ và hệ thức lượng trong tam giác vuông: \(v_{12}'=\dfrac{v_{23}'}{cos\hat{ADB}}=\dfrac{2}{cos60^o}=4\left(m/s\right)\).
(c) Khi đi theo hướng \(AC\), vector \(\overrightarrow{v_{12}}\) hướng theo hướng vector \(\overrightarrow{AB}\)
\(\Rightarrow AB=v_{12}t=4\cdot100=400\left(m\right)\)
(d) Khi đi theo hướng \(AD\), vận tốc của thuyền so với bờ là \(v_{13}'=v_{12}'sin\hat{ADB}=4\cdot sin60^o=2\sqrt{3}\left(m/s\right)\)
Thời gian qua sông lần sau: \(t'=\dfrac{AB}{v_{13}'}=\dfrac{400}{2\sqrt{3}}\approx115,47\left(s\right)\)

