Question

mọi người ơi cho mình hỏi chỗ này với, mình biết là rút 3 ra để dùng công thức cộng của sin, mình bấm máy tính cũng ra 2 giá trị giống nhau, nhưng mà làm sao biết để rút như vậy được hả mọi người ơi cú tuiii 🥹

Answer 1

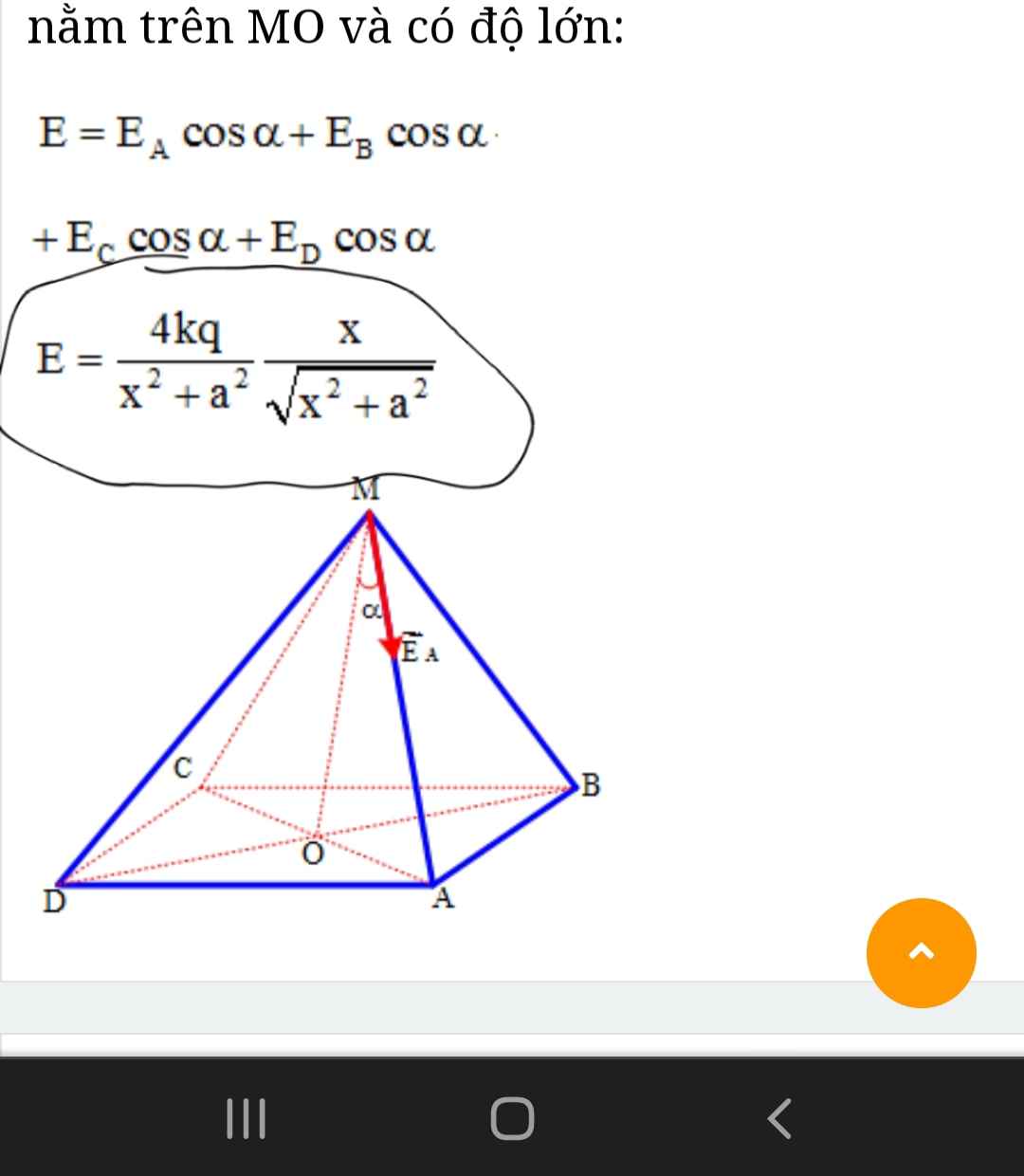
Khi bạn nhìn thấy biểu thức có dạng: `a sin x+b cos x` (chỗ này `2` cung là phải giống nhau) thì ta áp dụng cộng thức:

  `\sqrt{a^2+b^2}(a/\sqrt{a^2+b^2} sin x+b/\sqrt{a^2+b^2} cos x`

R ấn máy tính tìm giá trị của `sin` hoặc `cos` của `a/\sqrt{a^2+b^2}` và `b/\sqrt{a^2+b^2}`

 Nhưng cũng có trường hợp bạn ấn nó sẽ không ra giá trị của cung cụ thể thì bạn sẽ giả sử $\left[\begin{matrix} \dfrac{a}{\sqrt{a^2+b^2}}=sin \alpha\text{ và } \dfrac{b}{\sqrt{a^2+b^2}}=cos \alpha\\ \dfrac{a}{\sqrt{a^2+b^2}}=cos \alpha\text{ và } \dfrac{b}{\sqrt{a^2+b^2}}=sin \alpha\end{matrix}\right.$

   `->` R biến đổi thành công thức cộng, trừ của sin