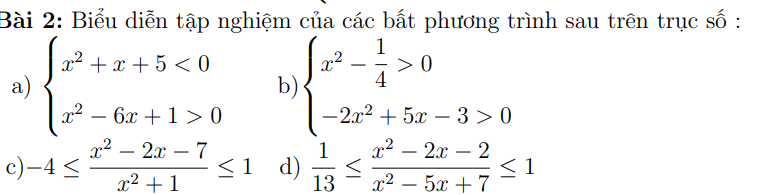\(\left(m-2\right)x^4-2\left(m+1\right)x^2+2m-1=0\left(1\right)\)
\(m=2\left(ktm\right)\)
\(m\ne2:đặt:x^2=t\ge0\Rightarrow\left(1\right)\Leftrightarrow\left(m-2\right)t^2-2\left(m+1\right)t+2m-1=0\)
\(3nghiem\Leftrightarrow\left\{{}\begin{matrix}2m-1=0\\t1+t2=\dfrac{2m+2}{m-2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m\in\phi\)
\(4nghiem\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\t1+t2>0\Leftrightarrow\\t1.t2>0\end{matrix}\right.\left\{{}\begin{matrix}\left(m+1\right)^2-\left(m-2\right)\left(2m-1\right)>0\\\dfrac{2m+2}{m-2}>0\\\dfrac{2m-1}{m-2}>0\end{matrix}\right.\)
giải hệ bất pt trên=>m
\(c3:b;\left\{{}\begin{matrix}-8\le x\le-2\\m\left(x-3\right)\ge1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-8\le x\le-2\\m\le\dfrac{1}{x-3}\end{matrix}\right.\)
\(có\) \(nghiệm\Leftrightarrow m\le max:\dfrac{1}{x-3}trên\left[-8;-2\right]\)
\(\Leftrightarrow m\le\dfrac{-1}{5}\)