Bài 2:
Vẽ đường tròn tâm A bán kính 4 cm thì đề phải là xác định vị trí các điểm B,C,D với $(A;4)$ chứ em?
Ta thấy:
$OA=2\sqrt{2}\Rightarrow AC=2OA=4\sqrt{2}$ cm
Vì $ABCD$ là hình vuông nên $AD=DC$. Xét tam giác vuông $ADC$ và áp dụng định lý Pitago:
$AD^2+DC^2=AC^2$
$AD^2+AD^2=(4\sqrt{2})^2$
$2AD^2=32\Rightarrow AD=4$
Vậy $AB=AD=4=R_{(A)}$ nên $B,D$ thuộc đường tròn $(A)$
$AC=4\sqrt{2}> R_{(A)}$ nên $C$ nằm ngoài đường tròn $(A)$
Bài 3:
Vì $B$ đối xứng với $D$ qua $AC$ nên $AC$ chính là đường trung trực của $BD$
$\Rightarrow AD=AB, CD=CB$
$\Rightarrow \triangle ABC=\triangle ADC$ (c.c.c)
$\Rightarrow \widehat{ADC}=\widehat{ABC}=90^0$
Tứ giác $ABCD$ có tổng 2 góc đối $\widehat{ABC}+\widehat{ADC}=90^0+90^0=180^0$ nên là tgnt
Hay $A,B,C,D$ cùng thuộc 1 đường tròn
b.
$AC=\sqrt{AB^2+BC^2}=\sqrt{6^2+8^2}=10$ (cm) theo định lý Pitago.
Gọi $M$ là trung điểm $AC$. Như vậy, tam giác $ABC$ có $BM$ là đường trung tuyến ứng với cạnh huyền $AC$ nên $BM=\frac{AC}{2}$
Tương tự, tam giác $ADC$ vuông tại $D$ có $DM$ là đường trung tuyến ứng với cạnh huyền $AC$ nên $DM=\frac{AC}{2}$
Vậy $BM=DM=\frac{AC}{2}=MA=MC$ nên $M$ là tâm đường tròn ngoại tiếp tứ giác $ABCD$
Bán kính: $R=\frac{AC}{2}=\frac{10}{2}=5$ (cm)
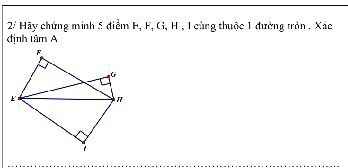giúp mình với ạ mình cảm ơn nhiều 
