a.
\(\Leftrightarrow\dfrac{2a}{2a+b}+\dfrac{2b}{2b+c}+\dfrac{2c}{2c+a}\le2\)
\(\Leftrightarrow\dfrac{2a}{2a+b}-1+\dfrac{2b}{2b+c}-1+\dfrac{2c}{2c+a}-1\le-1\)
\(\Leftrightarrow\dfrac{b}{2a+b}+\dfrac{c}{2b+c}+\dfrac{a}{2c+a}\ge1\)
Thật vậy, ta có:
\(VT=\dfrac{b^2}{2ab+b^2}+\dfrac{c^2}{2bc+c^2}+\dfrac{a^2}{2ca+a^2}\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
b.
Chuẩn hóa \(a+b+c=1\), BĐT cần chứng minh trở thành:
\(\dfrac{a}{\left(a+2b\right)^2}+\dfrac{b}{\left(b+2c\right)^2}+\dfrac{c}{\left(c+2a\right)^2}\ge1\)
Ta có:
\(\dfrac{a}{\left(a+2b\right)^2}+a\left(a+2b\right)+a\left(a+2b\right)\ge3a\)
Tương tự:
\(\dfrac{b}{\left(b+2c\right)^2}+b\left(b+2c\right)+b\left(b+2c\right)\ge3b\)
\(\dfrac{c}{\left(c+2a\right)^2}+c\left(c+2a\right)+c\left(c+2a\right)\ge3c\)
Cộng vế:
\(VT+2\left(a+b+c\right)^2\ge3\left(a+b+c\right)\)
\(\Leftrightarrow VT+2\ge3\)
\(\Leftrightarrow VT\ge1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
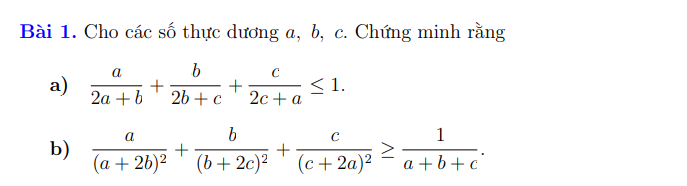


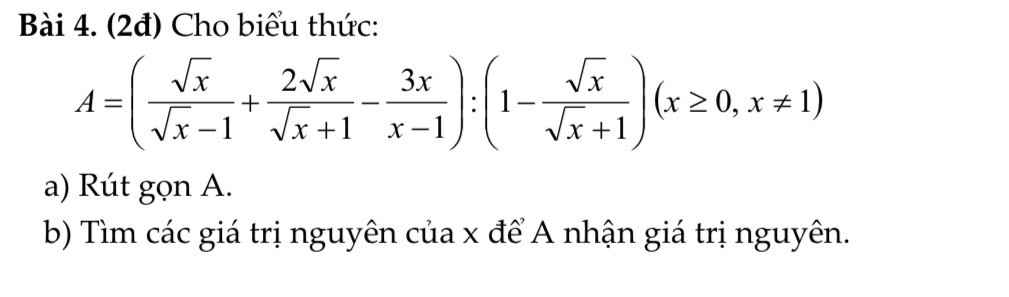

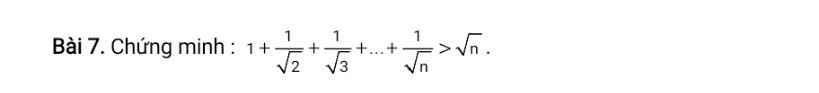
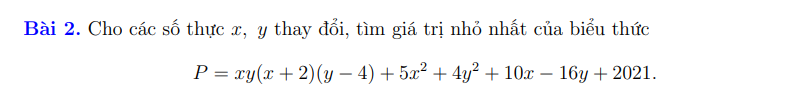
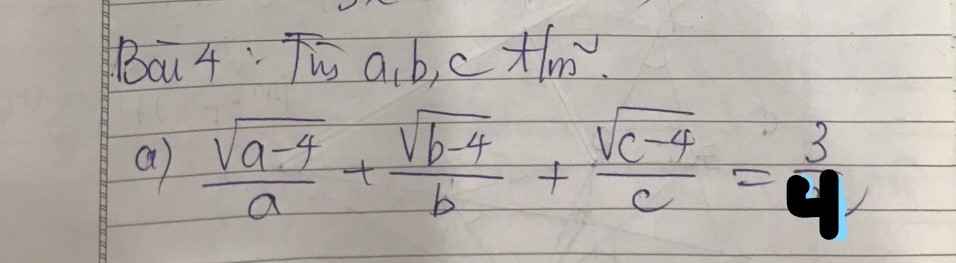
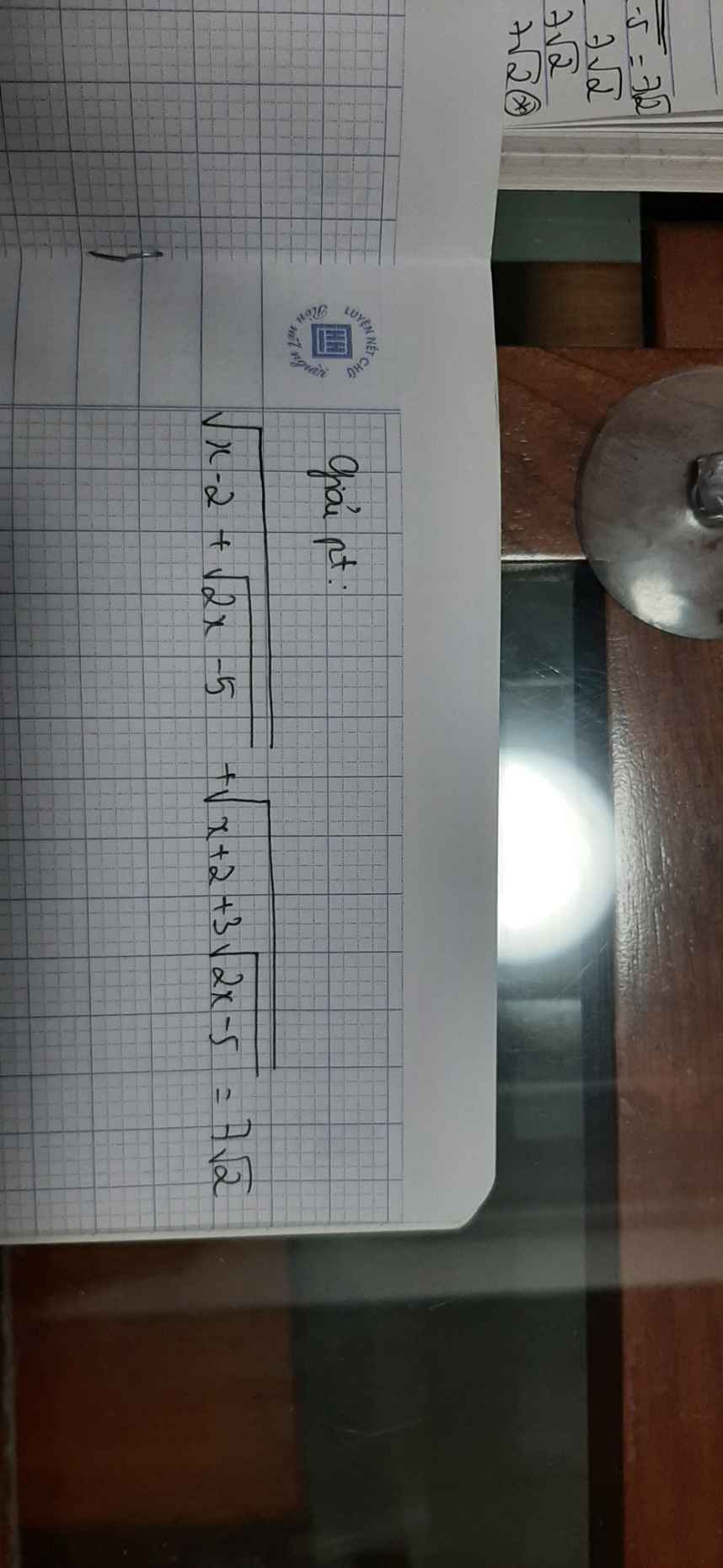

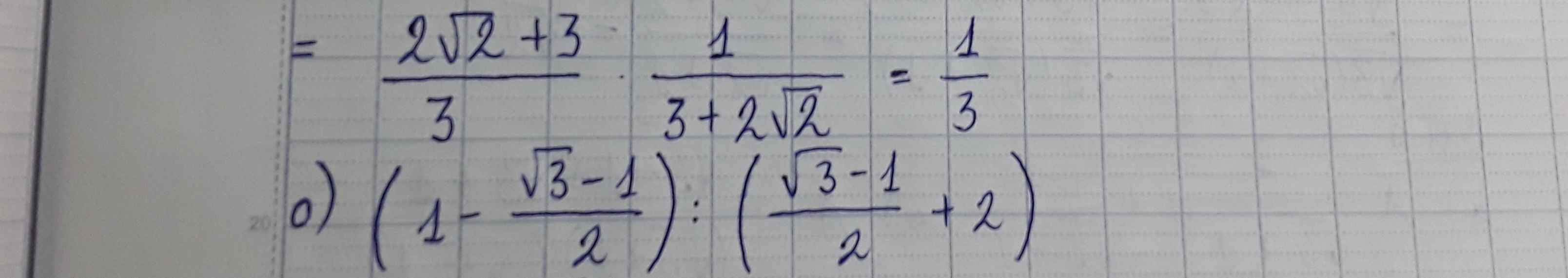 giải giúp mk câu o vs ạ
giải giúp mk câu o vs ạ