46.
ĐKXĐ: \(x\ne\dfrac{2}{3}\)
\(y'=\dfrac{4x\left(3x-2\right)-3\left(2x^2-1\right)}{\left(3x-2\right)^2}=\dfrac{6x^2-8x+3}{\left(3x-2\right)^2}\)
\(y''\left(x\right)=\dfrac{\left(12x-8\right)\left(3x-2\right)^2-6\left(3x-2\right)\left(6x^2-8x+3\right)}{\left(3x-2\right)^4}\)
\(y''=0\Rightarrow\left(12x-8\right)\left(3x-2\right)^2-6\left(3x-2\right)\left(6x^2-8x+3\right)=0\)
\(\Leftrightarrow\left(3x-2\right)\left[\left(12x-8\right)\left(3x-2\right)-6\left(6x^2-8x+3\right)\right]=0\)
\(\Leftrightarrow-2\left(3x-2\right)=0\)
\(\Leftrightarrow x=\dfrac{2}{3}\left(ktm\right)\)
Vậy pt đã cho vô nghiệm
44.
\(f'\left(x\right)=-\dfrac{mx^3}{3}+\dfrac{mx^2}{2}-\left(3-m\right)x\)
\(f''\left(x\right)=-x^2+mx+m-3\)
\(f'\left(x\right)\le0;\forall x\)
\(\Leftrightarrow\Delta=m^2+4\left(m-3\right)\le0\)
\(\Leftrightarrow m^2+4m-12\le0\)
\(\Rightarrow-6\le m\le2\)
45.
\(f'\left(x\right)=3cos3x+3sin3x\)
\(f''\left(x\right)=-9sin3x+9cos3x\)
\(f''\left(x\right)+a.f'\left(x\right)+b.f\left(x\right)=0\)
\(\Leftrightarrow-9sin3x+9cos3x+a.\left[3cos3x+3sin3x\right]+b.\left[sin3x-cos3x\right]=0\)
\(\Leftrightarrow\left(3a+b-9\right)sin3x+\left(3a-b+9\right)cos3x=0\)
\(\Rightarrow\left\{{}\begin{matrix}3a+b-9=0\\3a-b+9=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=0\\b=9\end{matrix}\right.\)
47.
\(f'\left(x\right)=2x-3\)
\(f''\left(x\right)=2\)
\(4.f'\left(x\right)-\left(2x-5\right).f''\left(x\right)-x+1=2\sqrt{25-x^2}\)
\(\Leftrightarrow4\left(2x-3\right)-2\left(2x-5\right)-x+1=2\sqrt{25-x^2}\)
\(\Leftrightarrow3x-1=2\sqrt{25-x^2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-1\ge0\\\left(3x-1\right)^2=4\left(25-x^2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{3}\\13x^2-6x-99=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{33}{13}\left(loại\right)\end{matrix}\right.\)
Pt đã cho có 1 nghiệm
48.
\(f'\left(x\right)=x^3+x^2+2\left(m+2\right)x+m\)
\(f''\left(x\right)=3x^2+2x+2m+4\)
\(f''\left(x\right)>0;\forall x\Rightarrow\Delta'=1-3\left(2m+4\right)< 0\)
\(\Leftrightarrow m>-\dfrac{11}{6}\)
\(\Rightarrow10-\left(-1\right)+1=12\) giá trị m nguyên
49.
\(g\left(x\right)=f\left(f\left(x\right)\right)\Rightarrow g'\left(x\right)=f'\left(f\left(x\right)\right).f'\left(x\right)\)
\(g''\left(x\right)=f''\left(x\right).f'\left(f\left(x\right)\right)+\left[f'\left(x\right)\right]^2.f''\left(f\left(x\right)\right)\)
Pt tương đương:
\(\left[f'\left(x\right)\right]^2.f''\left(f\left(x\right)\right)=f''\left(x\right).f'\left(f\left(x\right)\right)+\left[f'\left(x\right)\right]^2.f''\left(f\left(x\right)\right)\)
\(\Leftrightarrow f''\left(x\right).f'\left(f\left(x\right)\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}f''\left(x\right)=0\\f'\left(f\left(x\right)\right)=0\end{matrix}\right.\)
Từ đồ thị \(\Rightarrow f\left(x\right)\) có bậc 2 \(\Rightarrow f'\left(x\right)\) bậc nhất \(\Rightarrow f''\left(x\right)\) là hằng số
\(\Rightarrow f''\left(x\right)=0\) vô nghiệm
\(f'\left(f\left(x\right)\right)=0\Rightarrow f\left(x\right)=1\)
Từ đồ thị ta kẻ 1 đường ngang qua điểm \(y=1\) sẽ cắt đồ thị tại 2 điểm
\(\Rightarrow\) Pt đã cho có 2 nghiệm




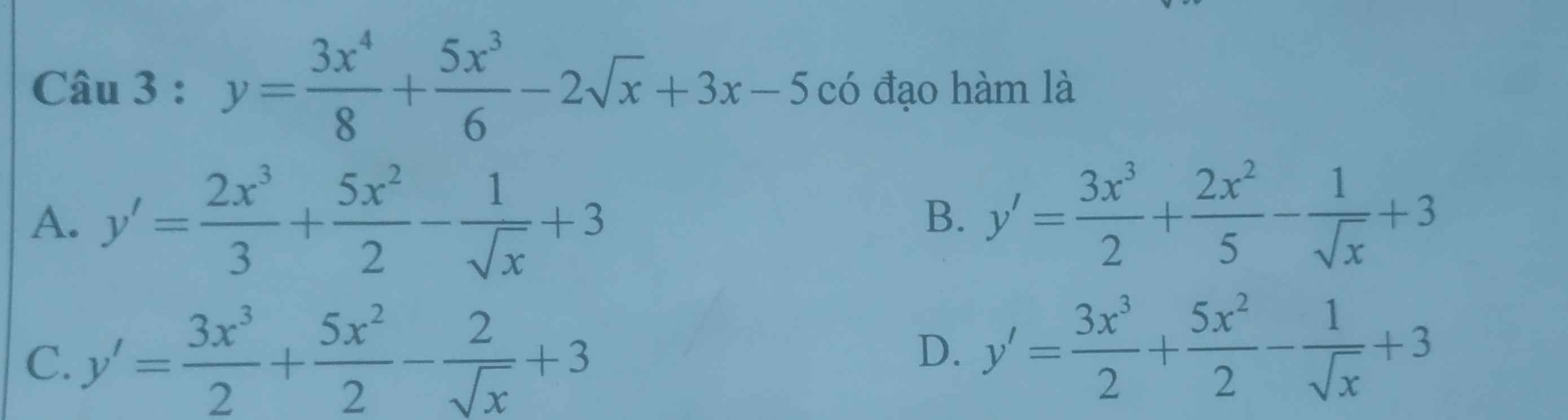 cho đáp án và giải thích giùm mình với ạ
cho đáp án và giải thích giùm mình với ạ