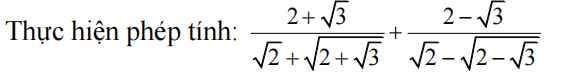Câu V:
a: Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot DB\)
=>\(\dfrac{AB^2}{AD^2}=\dfrac{BH\cdot BD}{DH\cdot DB}=\dfrac{BH}{DH}\)
=>\(\dfrac{BH}{DH}=\dfrac{CD^2}{BC^2}=\left(\dfrac{CD}{BC}\right)^2=\left(\dfrac{CD}{3CD}\right)^2=\dfrac{1}{9}\)
=>\(DH=9BH\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\)
=>\(9\cdot BH\cdot BH=\left(3\sqrt{10}\right)^2=90\)
=>\(BH^2=10\)
=>\(BH=\sqrt{10}\left(cm\right)\)
=>\(DH=9\sqrt{10}\left(cm\right)\)
\(BD=BH+DH=10\sqrt{10}\left(cm\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot BD\)
=>\(AB^2=\sqrt{10}\cdot10\sqrt{10}=100;AD^2=9\sqrt{10}\cdot\sqrt{10}=90\)
=>\(AB=10\left(cm\right);AD=3\sqrt{10}\left(cm\right)\)
Chu vi hình chữ nhật ABCD là:
\(C_{ABCD}=\left(AB+AD\right)\cdot2=\left(10+3\sqrt{2}\right)\cdot2\left(cm\right)\)
b: Xét ΔHAD có
M,I lần lượt là trung điểm của HD,HA
=>MI là đường trung bình của ΔHAD
=>MI//AD
Ta có: MI//AD
AB\(\perp\)AD
Do đó: MI\(\perp\)AB
Xét ΔMAB có
MI,AH là các đường cao
MI cắt AH tại I
Do đó: I là trực tâm của ΔMAB
=>BI\(\perp\)AM