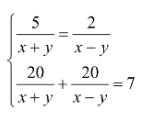Đặt 1/(x+y)=a; 1/(x-y)=b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}5a-2b=0\\20a+20b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{10}\\b=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=10\\x-y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=3\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+y}=a\\\dfrac{2}{x-y}=b\end{matrix}\right.\) \(ĐK:x+y\ne0;x-y\ne0\)
hpt trở thành:
\(\left\{{}\begin{matrix}5a-2b=0\\20a+20b=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{10}\\b=\dfrac{1}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{10}\\\dfrac{1}{x-y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=10\\x-y=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=3\end{matrix}\right.\)