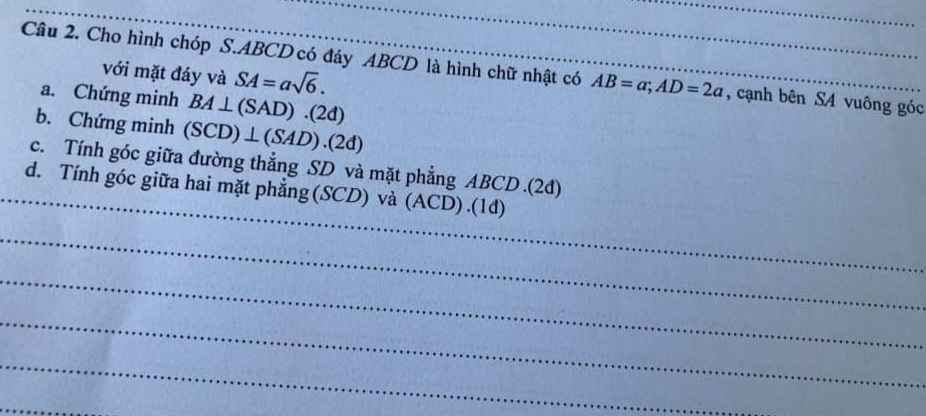3.
a.
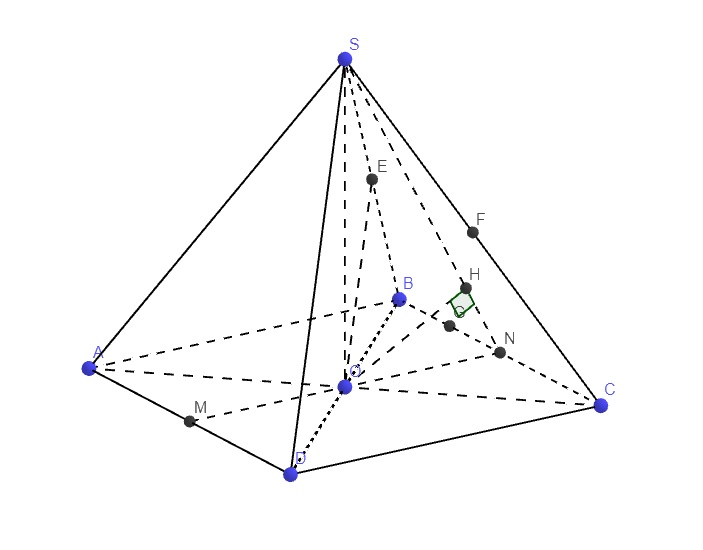
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\\BD\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SO\perp BD\)
\(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\)
b.
M là trung điểm AD, N là trung điểm BC \(\Rightarrow MN||AB\Rightarrow MN\perp BC\)
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
Mà \(SO\in\left(SMN\right)\Rightarrow BC\perp\left(SMN\right)\)
\(\Rightarrow BC\perp SM\)
Lại có \(OH\in\left(SMN\right)\Rightarrow BC\perp OH\)
Theo giả thiết \(OH\perp SN\)
\(\Rightarrow OH\perp\left(SBC\right)\Rightarrow OH\perp SB\)
c.
\(\left\{{}\begin{matrix}AC\perp BD\\SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\)
Hay \(OC\perp\left(SBD\right)\)
\(\Rightarrow\) Góc giữa (SBC) và (SBD) là góc giữa 2 đường thẳng OC và OH
Hay \(\left(\left(SBD\right),\left(SBD\right)\right)=\widehat{COH}\)
\(OB=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow SO=\sqrt{SB^2-OB^2}=\dfrac{a\sqrt{6}}{2}\)
\(ON=\dfrac{1}{2}AB=\dfrac{a}{2}\Rightarrow OH=\dfrac{SO.ON}{\sqrt{SO^2+ON^2}}=\dfrac{a\sqrt{42}}{14}\)
\(OH\perp\left(SBC\right)\Rightarrow OH\perp CH\Rightarrow\Delta OCH\) vuông tại H
\(\Rightarrow cos\widehat{COH}=\dfrac{OH}{OC}=\dfrac{OH}{OB}=\dfrac{\sqrt{21}}{7}\)
\(\Rightarrow\widehat{COH}\approx49^06'\)
3d.
Gọi E là trung điểm SB \(\Rightarrow\) OE là đường trung bình tam giác SBD
\(\Rightarrow OE||SD\)
\(\Rightarrow\left(OH,SD\right)=\left(OH,OE\right)=\widehat{EOH}\)
\(OE=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\) (trung tuyến ứng với cạnh huyền)
\(OH\perp\left(SBC\right)\Rightarrow OH\perp EH\Rightarrow\Delta OEH\) vuông tại H
\(cos\widehat{EOH}=\dfrac{OH}{OE}=\dfrac{\sqrt{21}}{7}\Rightarrow\widehat{EOH}\approx49^06'\)
e.
Gọi F là trung điểm SC, G là trung điểm BN
\(\Rightarrow OF\) là đường trung bình tam giác SAC và OG là đường trung bình tam giác BDN
\(\Rightarrow\left\{{}\begin{matrix}OF||SA\\OG||DN\end{matrix}\right.\) \(\Rightarrow\left(SA,DN\right)=\left(OF,OG\right)=\widehat{FOG}\)
\(OF=\dfrac{1}{2}SA=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\)
\(OG=\dfrac{1}{2}DN=\dfrac{1}{2}\sqrt{DC^2+CN^2}=\dfrac{a\sqrt{5}}{4}\)
\(cos\widehat{SCN}=\dfrac{CN}{SC}=\dfrac{\sqrt{2}}{4}\)
\(CF=\dfrac{1}{2}SC=\dfrac{a\sqrt{2}}{2}\) ; \(CG=CN+NG=\dfrac{3}{4}BC=\dfrac{3a}{4}\)
\(\Rightarrow GF=\sqrt{CF^2+CG^2-2CF.CG.cos\widehat{SCN}}=\dfrac{a\sqrt{11}}{4}\)
\(\Rightarrow cos\widehat{FOG}=\dfrac{OF^2+OG^2-FG^2}{2OF.OG}=\dfrac{\sqrt{10}}{20}\)
\(\Rightarrow\widehat{FOG}\approx80^054'\)
4.
a.
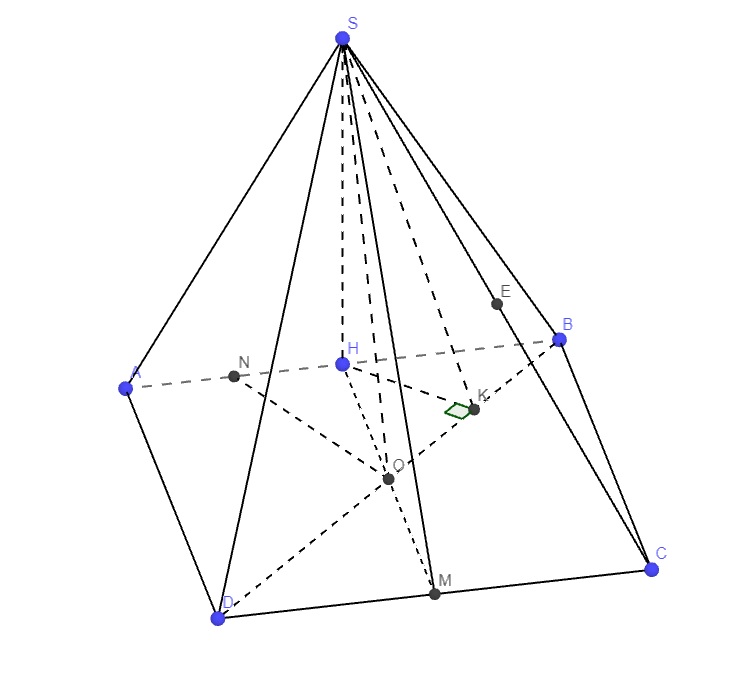
SAB đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow SH\perp\left(ABCD\right)\)
\(BC\in\left(ABCD\right)\)\(\Rightarrow SH\perp BC\)
Lại có \(BC\perp AB\) (gt)
\(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
b.
Gọi M là trung điểm CD
\(\Rightarrow HM||BC\Rightarrow HM\perp AB\)
\(SH\perp\left(ABCD\right)\Rightarrow SH\perp AB\)
\(\Rightarrow AB\perp\left(SHM\right)\)
Lại có \(DC||AB\Rightarrow DC\perp\left(SMH\right)\)
Mà \(DC=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SMH}\) là góc giữa (SCD) và (ABCD)
\(SH=\dfrac{2a\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(HM=AD=2a\)
\(\Rightarrow tan\widehat{SMH}=\dfrac{SH}{HM}=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{SMH}\approx40^053'\)
4c.
Từ H kẻ \(HK\perp BD\)
\(SH\perp\left(ABCD\right)\Rightarrow SH\perp BD\)
\(\Rightarrow BD\perp\left(SHK\right)\)
Mà \(BD=\left(SBD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SKH}\) là góc giữa (SBD) và (ABCD)
\(OB=\dfrac{1}{2}BD=a\sqrt{2}\)
\(\Rightarrow HK=\dfrac{1}{2}OB=\dfrac{a\sqrt{2}}{2}\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow tan\widehat{SKH}=\dfrac{SH}{HK}=\sqrt{6}\)
\(\Rightarrow\widehat{SKH}\approx67^047'\)
d.
Gọi N là trung điểm AH \(\Rightarrow ON\) là đường trung bình tam giác HAM
\(\Rightarrow ON||AM\Rightarrow\left(SO,AM\right)=\left(SO,ON\right)=\widehat{SON}\)
\(NH=\dfrac{1}{2}AH=\dfrac{1}{4}AB=\dfrac{a}{2}\)
\(OH=\dfrac{1}{2}HM=\dfrac{1}{2}AD=a\)
\(ON=\sqrt{NH^2+OH^2}=\dfrac{a\sqrt{5}}{2}\)
\(SO=\sqrt{SH^2+OH^2}=2a\)
\(SN=\sqrt{SH^2+NH^2}=\dfrac{a\sqrt{13}}{2}\)
\(cos\widehat{SON}=\dfrac{SO^2+ON^2-SN^2}{2SO.ON}=\dfrac{\sqrt{5}}{5}\)
\(\Rightarrow\widehat{SON}\approx63^026'\)
e. Điểm I là điểm nào nhỉ? Đề bài hình như bị thiêys