Chương 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
Các câu hỏi tương tự
chứng minh rằng trong một hình bình hành , tổng bình phương các cạnh bằng tổng bình phương của 2 đường chéo .
.Cho tam giác ABC có A(4;3) , B(0; 5) , C(6; 2) .
a) Chứng minh :ABC vuông tại B . Tính diện tích tam giác ABC.
b) Tìm tọa độ điểm K là chân đường cao kẻ từ B của tam giác ABC.
c) Tìm tọa độ điểm I là tâm đường tròn ngoại tiếp tam giác ABC.
d) Tìm tọa độ điểm J là tâm đường tròn nội tiếp tam giác ABC.
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức (1.0 điểm). Chứng minh đẳng thức .
Đọc tiếp
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức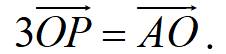
(1.0 điểm). Chứng minh đẳng thức .
Cho tứ giác ABCD nội tiếp (O;R). AC vuông góc với BD và AC cắt BD tại I. Gọi trung điểm của AB là M. Chứng minh rằng MI vuông góc với DC
cho 4 điểm bất kỳ A , B , C ,D .Chứng minh rằng : vector DA nhân vector BC + vector DB nhân vector CA + vector DC nhân vector AB = 0 . Từ đó suy ra một cách chứng minh định lý : '' 3 đường cao của một tam giác đồng quy''
gọi H là trực tâm của tam giác không vuông ABC . Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác ABC , HBC . HCA . HAB bằng nhau
cho tứ giác ABCD . Gọi M , N lần luợt là trung điểm của AC và BD . Chứng minh rằng : AB2 + BC2 + CD2 +DA2 = AC2 + BD2 + 4MN2
cho 2 đường tròn ( O ; R ) và ( O1 ; R1 ) cắt nhau tại 2 điểm A và B . Trên đường thẳng AB , lấy điểm C ở ngoài 2 đường tròn và kẻ 2 tiếp tuyến CE , CF đến 2 đường tròn đó ( E , F là các tiếp điểm ) . Chứng minh rằng CE = CF
trong mạt phẳng Oxy cho tam giác ABC có A(-1,0) , B(1,2) , C(5,-2) : a) hỏi tam giác ABC là tam giác gì ? Tính diện tích tam giác ABC ; b) gọi H là chân đường cao kẻ từ B của tam giác ABC . Tìm tọa độ của H .
