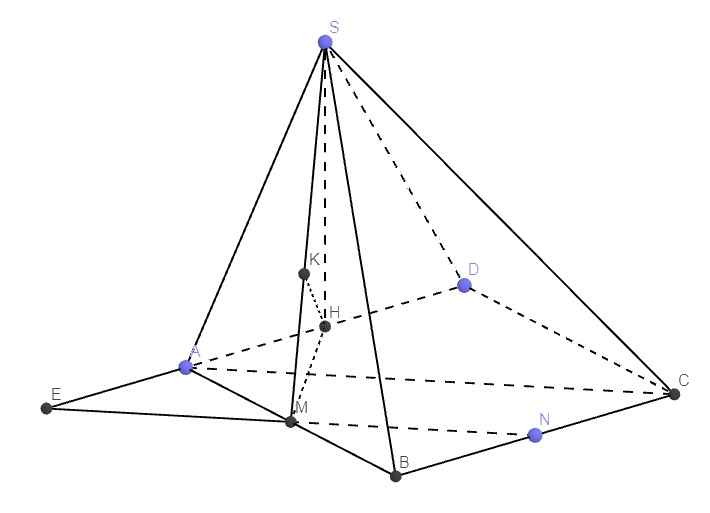
Gọi H là trung điểm AD \(\Rightarrow SH\perp\left(ABCD\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Qua M kẻ đường thẳng song song AC cắt AD kéo dài tại E
\(\Rightarrow AC||\left(SME\right)\Rightarrow d\left(AC;SM\right)=d\left(AC;\left(SME\right)\right)=d\left(A;\left(SME\right)\right)\)
\(AE=\dfrac{1}{2}EH\Rightarrow d\left(A;\left(SME\right)\right)=\dfrac{1}{2}d\left(H;\left(SME\right)\right)\)
Các tam giác AHM và AEM vuông cân tại A \(\Rightarrow\Delta EHM\) vuông cân tại M
\(\Rightarrow EM\perp HM\Rightarrow EM\perp\left(SHM\right)\)
Từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SME\right)\)
\(\Rightarrow HK=d\left(H;\left(SME\right)\right)\)
\(MH=AH\sqrt{2}=\dfrac{a\sqrt{2}}{2}\)
Áp dụng hệ thức lượng: \(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{MH^2}=\dfrac{10}{3a^2}\Rightarrow HK=\dfrac{a\sqrt{30}}{10}\)
\(\Rightarrow d\left(SM;AC\right)=\dfrac{1}{2}HK=\dfrac{a\sqrt{30}}{20}\)