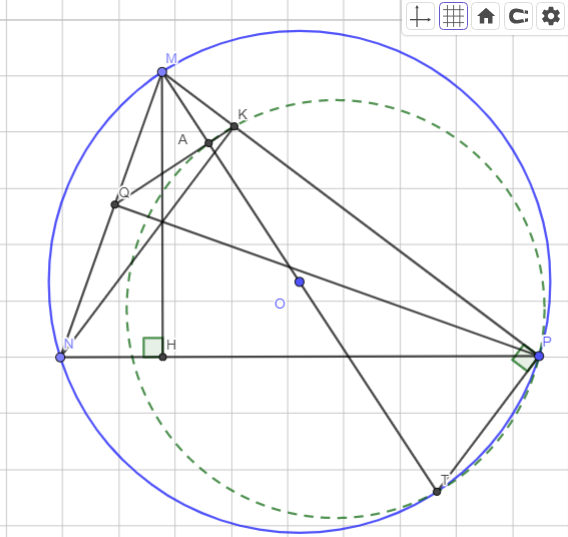
Xét $\Delta MNH$ và $\Delta P$ ta có:
$\large \widehat{MHN}=\widehat{MPT}=90^o$
$\large \widehat{MNP}=\widehat{MTP}$(Hai góc cùng chắn cung $MP$)
Do đó $\large \Delta MNH \sim \Delta MTP$ $(g-g)$
Từ đó: $\frac{MN}{MT}=\frac{MH}{MP}\Leftrightarrow MN.MP=MH.MT$
Xét tứ giác $NQKP$ ta có:
$\large \widehat{NQP}=\widehat{PKN}=90^o$
Mà hai góc này cùng chắn cung $NP$
Do đó tứ giác $NQKP$ là tứ giác nội tiếp
Suy ra: $\large \widehat{PKQ}+\widehat{PNQ}=180^o$ (Hai góc nội tiếp đối nhau)
Đồng thời ta có $\large \widehat{PKQ}+\widehat{MKQ}=180^o\Rightarrow \widehat{MNP}=\widehat{MTP}=\widehat{MKQ}$
Gọi $A$ là giao điểm của $QK$ và $MT$
Xét tứ giác $TPKA$ ta có:
$\large \widehat{MTP}+\widehat{PKQ}=\widehat{PKQ}+\widehat{MKQ}=180^o$
Mà hai góc này ở vị trí đối nhau nên tứ giác $TPAK$ là tứ giác nội tiếp
$\large \Leftrightarrow \widehat{MPT}+\widehat{TAK}=180^o\Leftrightarrow \widehat{TAK}=180^o-\widehat{MPT}=90^o$
Do đó $MT$ vuông góc với $QK$
Hình: