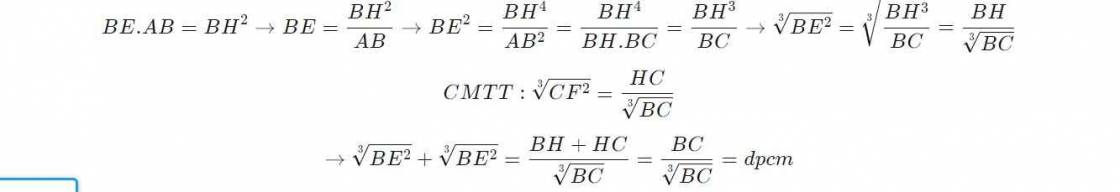Question

cho tam giác ABC vuông tại A, đường cao AH. gọi E,F lần lượt là hình chiếu của H trên AB, AC. gọi M là trung điểm của BC.

1,chứng minh \(\widehat{AEF}=\widehat{MAC}\)

2, chứng minh \(\sqrt[3]{BE^2}+\sqrt[3]{CF^2}=\sqrt[3]{BC^2}\)

3, Gỉa sử BC=a (không đổi). tìm gtnn của \(BE^2+CF^2\)

Answer 1

Akai Haruma Nguyễn Thanh Hằng Mashiro Shiina

Answer 2

1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ

nên AEHF là hình chữ nhật

Suy ra: góc AEF=góc AHF=góc C(1)

Ta có: ΔABC vuông tại A

mà AM là đường trung tuyến

nên MA=MC

=>góc MAC=góc MCA(2)

Từ (1) và (2) suy ra góc AEF=góc C

2: Tham khảo: