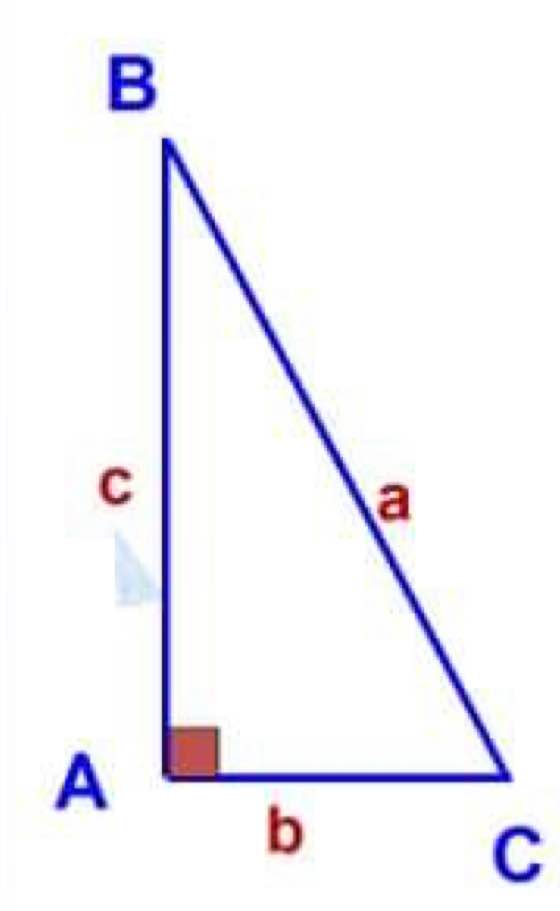
pytago=>\(BC=\sqrt{AB^2+AC^2}=10cm\)
\(=>\sin B=\dfrac{AC}{BC}=\dfrac{8}{10}=0,8=\cos C\)
\(=>\cos B=\dfrac{AB}{BC}=\dfrac{6}{10}=0,6=\sin C\)
\(=>\tan B=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}=\cot B\)
\(=>\cot B=\dfrac{AB}{AC}=\dfrac{3}{4}=\tan C\)
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(\Rightarrow sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
\(cosB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{4}{3}\)
\(cotB=\dfrac{AB}{AC}=\dfrac{3}{4}\)
Do tam giác ABC vuông tại A \(\Rightarrow C=90^0-B\)
\(\Rightarrow sinC=sin\left(90^0-B\right)=cosB=\dfrac{3}{5}\)
\(cosC=cos\left(90^0-B\right)=sinB=\dfrac{4}{5}\)
\(tanC=tan\left(90^0-B\right)=cotB=\dfrac{3}{4}\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\)